自由落下(CUI)
純粋なODEを知るために、3Dアニメーションなしの簡単なプログラムを用意しました。
下記のプログラムを実行すると、z数値がどんどん小さくなる(落下する)ことが確認できます。
#include <ode/ode.h>
#include <stdio.h>
static dWorldID world;
static dBodyID body0;
int main(int argc, char* argv[])
{
dInitODE();
world = dWorldCreate();
dWorldSetGravity( world, 0.0, 0.0, -9.8 );
body0 = dBodyCreate( world );
dBodySetPosition( body0, 0.0, 0.0, 10.0 );
// simulation
for (int i=0; i<10000; i++) {
dWorldStep( world, 0.001 );
const dReal *pos = dBodyGetPosition( body0 );
printf( "x=%f, y=%f, z=%f\n", pos[0], pos[1], pos[2] );
}
dWorldDestroy( world );
dCloseODE();
return 0;
}
- プログラムの流れ
- ODEの初期化:dInitODE()
- 世界の生成:dWorldCreate()
- 世界に重力を設定:dWorldSetGravity()
- 物体を生成:dBodyCreate()
- 物体の位置を設定:dBodySetPosition()
- シミュレーションを進行:dWorldStep() <=繰り返し
- 世界の破棄:dWorldDestroy()
- ODEの終了:dCloseODE()
ODEは本当にSI単位系?
ODEは本当にSI単位系?っていうのを疑問に持ったので、
物体の落下を基に運動方程式が当てはまるかどうか検証してみました。
(今さらって感じもしますが)
物体の落下を基に運動方程式が当てはまるかどうか検証してみました。
(今さらって感じもしますが)
運動方程式
ニュートンの原理より落下の運動方程式は次のとおり。
両辺からmを削除。
これより質量は落下に関係ないことがわかります。
それで、この式に2回ほど積分をかけていくと、次のような式となります。
y(t)は時間tにおける位置となります。
y(0)は時間0における位置です。
y(0)は時間0における位置です。
検証
物体の初期位置y(0)=10としたとき、y(t)=0(地面上)となる時間は、
g=9.8とすると、t=1.42857 (秒)
早速検証してみます。
z座標が0未満となったときシミュレーションを停止するプログラムを用意しました。
z座標が0未満となったときシミュレーションを停止するプログラムを用意しました。
#include <ode/ode.h>
#include <stdio.h>
static dWorldID world;
static dBodyID body0;
#define STEP_SIZE 0.0001 // シミュレーションステップサイズを定義
int main(int argc, char* argv[])
{
double time = 0.0;
dInitODE();
world = dWorldCreate();
dWorldSetGravity( world, 0.0, 0.0, -9.8 ); // 重力加速度g=9.8
body0 = dBodyCreate( world );
dBodySetPosition( body0, 0.0, 0.0, 10.0 ); // 初期位置(高さ)z=10
// simulation
for (int i=0; i<100000; i++) {
dWorldStep( world, STEP_SIZE );
time += STEP_SIZE;
const dReal *pos = dBodyGetPosition( body0 );
printf( "time=%f : x=%f, y=%f, z=%f\n", time, pos[0], pos[1], pos[2] );
if (pos[2] < 0) break; // 位置がゼロ(地面上)となったときシミュレーション停止
}
dWorldDestroy( world );
dCloseODE(); // VCEEの場合はブレイクポイントを打ってね!
return 0;
}
結果
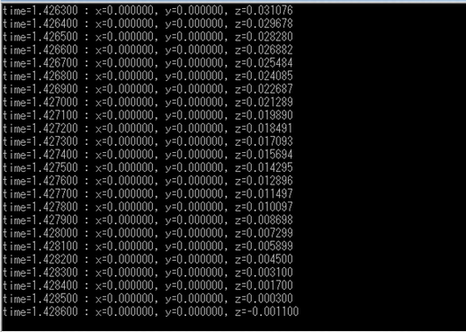
おお、およそ1.286(秒)のようです。
以上
添付ファイル
