前回のつづきです.
2) spline interpolation
前回は,一次関数のアルゴリズムでデータの補間を行いました.今回は,より自然な変化に近づけるため,多項式を用いたスプライン補間(spline interpolation)を行いたいと思います.以下の手順によりRで作業していきます.
Rを立ち上げてください.
前回と同様に元データを読み込み確認します.
ice <- read.table("ice(fileのパス)",sep = "\t",header = T)
ls()
ice
元データの列を定義していきます.
x <- ice[,1] …1列目の時間軸をxと定義
x …xを表示
y <- ice[,2] …2列目の物理量をyと定義
y
データを等間隔にします.
xnew <- seq(1000,414000,1000) …1000~414000の数を1000刻みにしたものをxnewと定義
xnew …xnewを表示
ここから,スプライン補間をおこなっていきます.
その前に,Rの検索エンジンを使って今回行うスプライン補間を検索します.
(C:)ドライブ → Program Files → R → doc → search → SearchEngine.html
を開いてください.そうすると,Rの検索エンジンにつながります.
ここでは,使用例を紹介してくれるので,Rでわからないことがあれば,この検索エンジンを使ってみてください.
(このページが今後すぐ利用できるようにおすすめに保存しておくと良いでしょう.)
検索欄にinterpolationと入れてみてください.Rで行えるさまざまな補間法が紹介されます.
その中にakimaという方による補間法があったので,今回はこれを使用します.
では,Rの作業画面に戻ってください.
まず,akimaによるスプライン補間を行えるようにするためにパッケージをインストールします.
画面上の"パッケージ" → パッケージのインストール → "Japan"を選択 → "akima"を選択
つづいて,
library(akima) …パッケージakimaを利用する
ynew <- aspline(x,y,xnew) …aspline関数でスプライン補間した物理量をynewと定義
plot(ynew,type="o")
lines(ice,col="red")
で,以下のようなグラフができます.
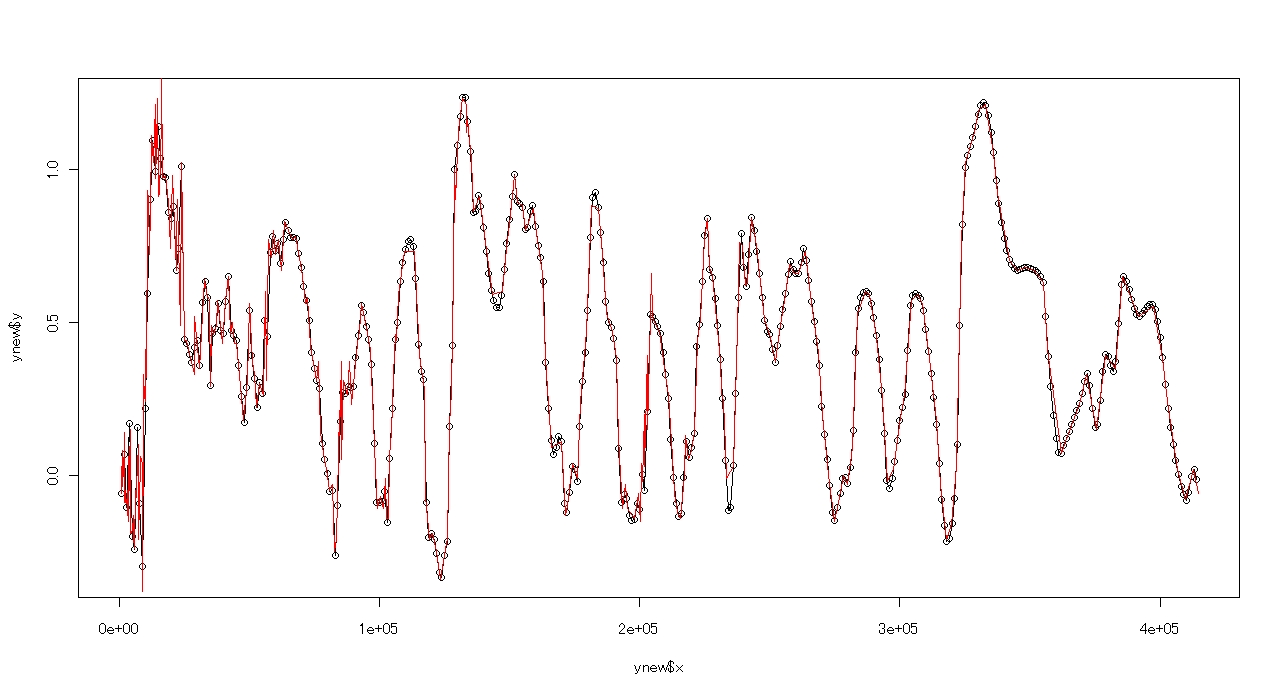
みやすいグラフに修正していきます.
plot(ice,type="o",xlim = c(420000,0),ylim = c(1.5,-0.5))
lines(ice,col="red")
以上より,下のようなグラフが出来上がります.
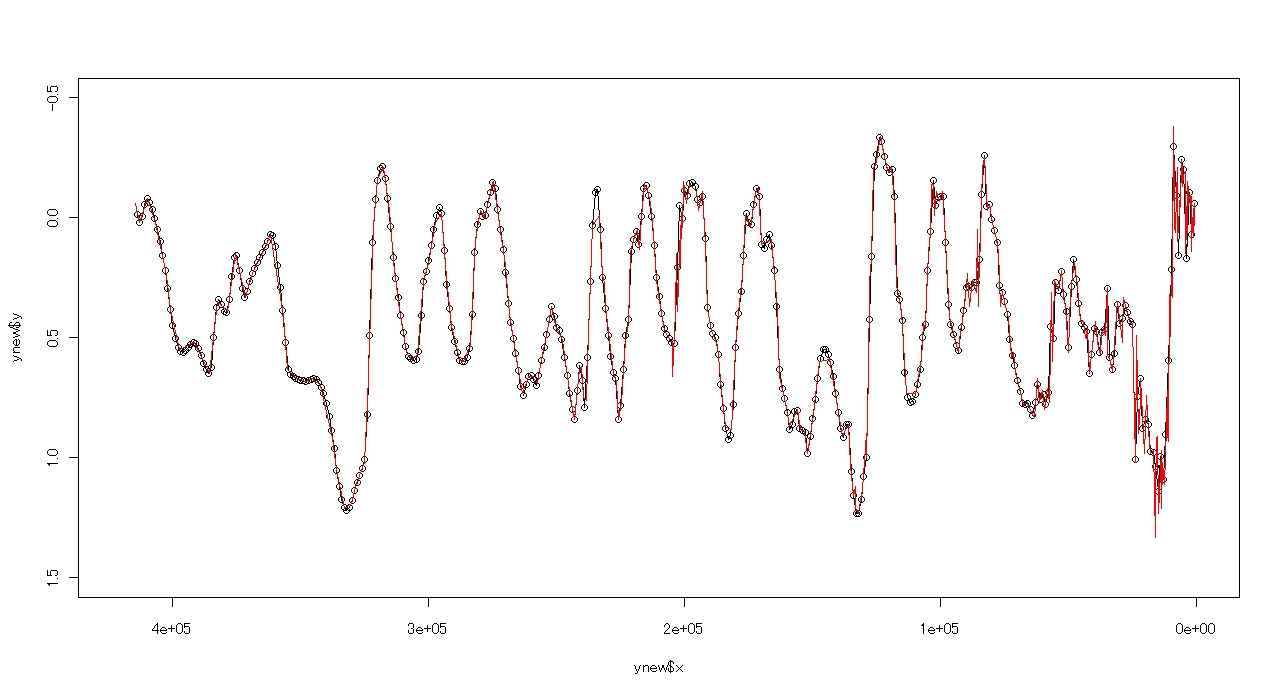
3 波にフィルタをかける
interpolationによってできたグラフで表される波は,さまざまな周波数から成っています.そのため,周波数の階級を分けることで,用途に応じた解析が可能になります.例えば,高周波の振動を抽出する(これをHigh Pass Filterといいます.)と細かい変動をみることができます.逆に,低周波の振動を残す(これをLow Pass Filterいいます.)と大きな流れをみることができます.今回は,Low Pass Filterをかけて大きな流れをみてみたいと思います.ここでは,移動平均(Movung AverageまたはRunning Mean)によって表していきます.
5個の移動平均を表示する
w <- rep(1/5,5) …rep関数を用い5個の平均を計算していくものをwと定義
y5 <- filter(ynew$y,w) …ynewに対してwを実行したものをy5と定義
lines(xnew,y5)
以上より,5個の移動平均のグラフ(細い黒線)が付け加えられます.
(みやすくするため巨大に表示しました.↓ )
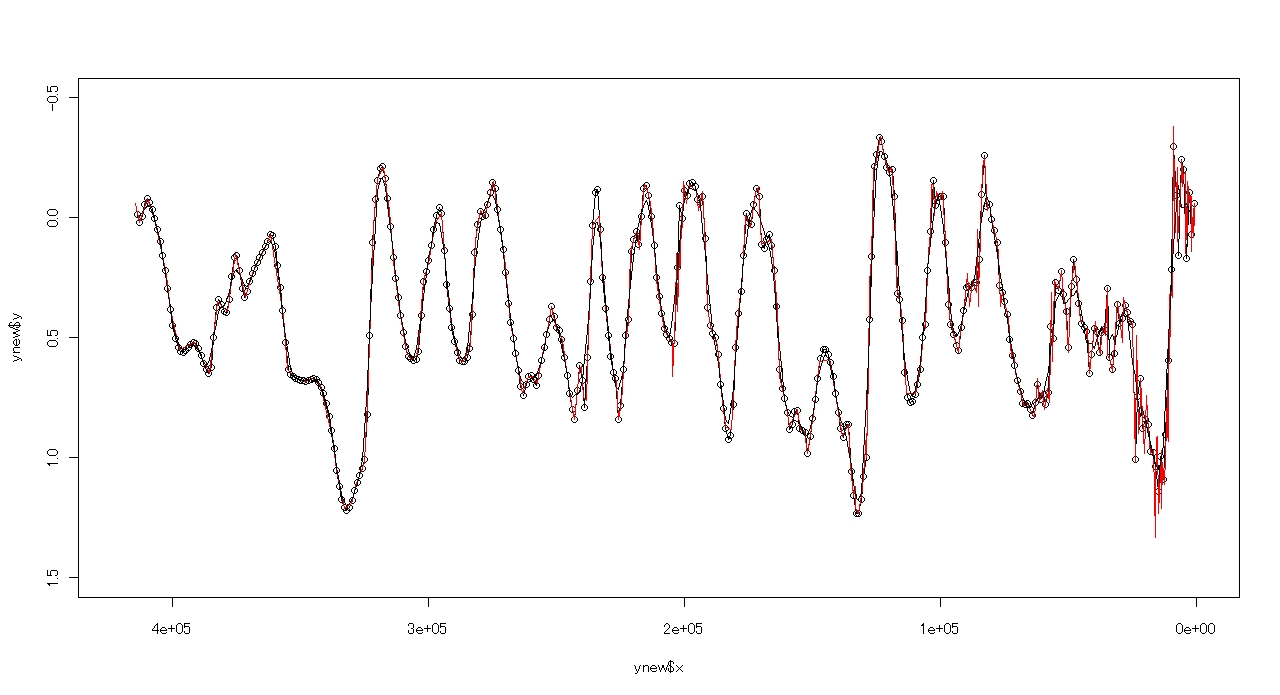
10個の移動平均を表示する
y10 <- filter(ynew$y,rep(1/11,11))
lines(xnew,y10,lwd="3")
以上より,下のように10個の移動平均のグラフ(太い黒線)が付け加えられます.
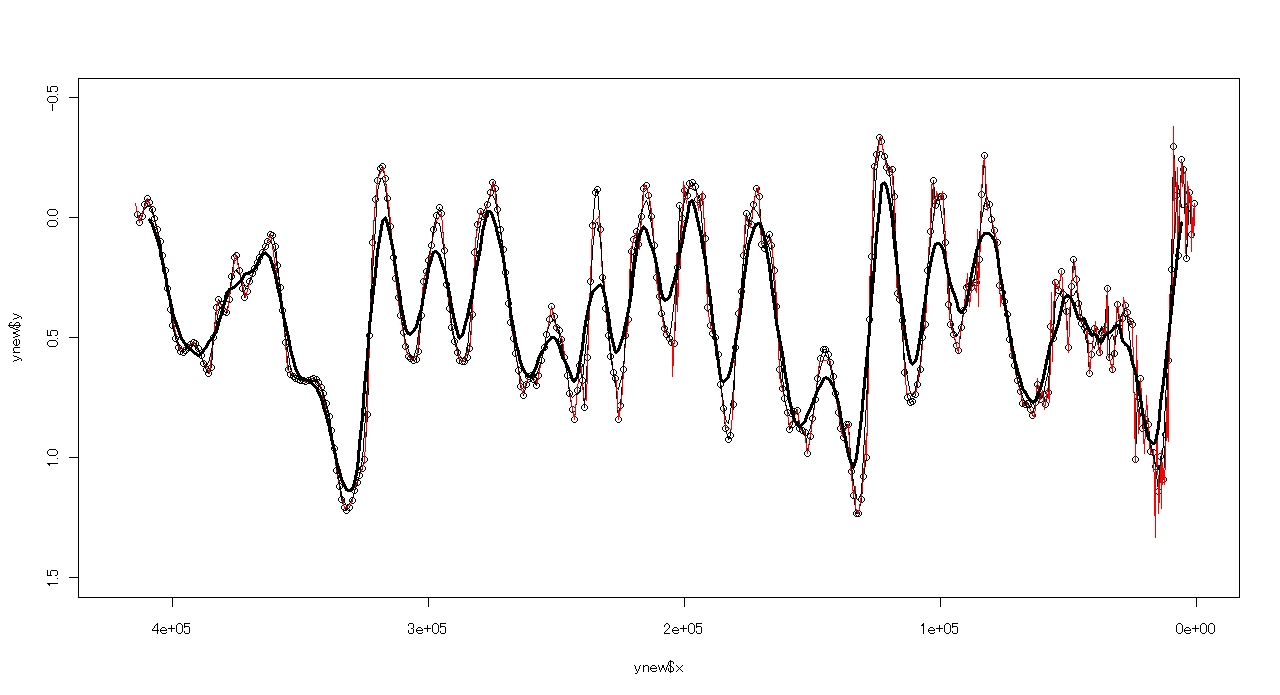
今回は,とりあえずここまでになります.終了するときは,
q()
で終えてください.この際,保存しておくと,今までのRの作業を後でみることができます.
保存したものをみたいときは,
(C:)ドライブ → Program Files → R → bin → R.history
より確認できます.
最終更新:2009年04月23日 13:56



