2009-4-2:時系列解析③ 自己相関関数をみる - BioEoS::環境解析学研究室::

4　Auto Correlation Function

　相関というと，“気温と降水量の関係”のように異なる物理量の関係が連想されることとおもいます．しかしここでは，一つの時系列内で時間的に離れた2点の相関をみたいとおもいます．このような関数を自己相関関数（Auto Correlation Function）といいます．よって，例えば時系列が1万年周期をもっていた場合，１万年を隔てた2点の相関係数は1になります．

それでは，Rでの作業に入りたいとおもいます．

データを時系列として認識させる

自己相関を表示させる前に，データを時系列としてRに認識させます．

ice1000 <- read.table("ice1000",header = T)

以前，線形補間で作成したice1000というファイルを読み込みます．

ice1000　　　　　　　　　　　　　　　　　　　　　　　　　　　･･･ice1000 を表示
ice_t <- ts(ice1000[,2],start = 1,frequency = 1)　　･･･ice1000 の2列目を時系列として認識し，ice_t と定義
ts.plot(ice_t)　　　　　　　　　　　　　　　　　　　　　　　　･･･時系列 ice_t をプロットする

するとこのようなグラフができます．

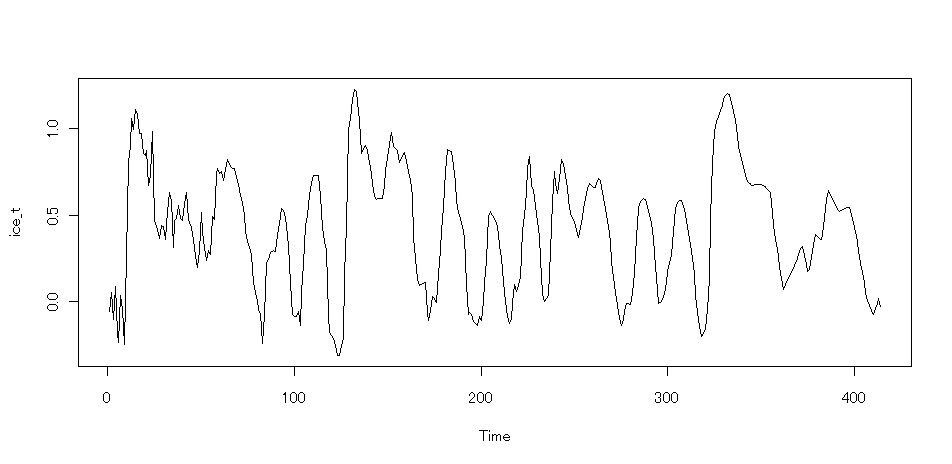
自己相関係数の計算

acf(ice_t)　　　　　　　　　　　　･･･ice_t の自己相関係数を計算
acf(ice_t,lag.max = 150)　　･･･lag.maxで計算領域を指定

作成したものを並べて表示する

par(mfrow = c(行数,列数))より，グラフの行列を指定して表示することができます．

par(mfrow = c(2,1))　　　　　　　･･･2行1列でグラフを表示する
ts.plot(ice_t)　　　　　　　　　　　･･･1行目に ice_t を表示
acf(ice_t,lag.max = 150)　　　　･･･2行目に ice_t の自己相関を表示

すると，次のように表示されます.

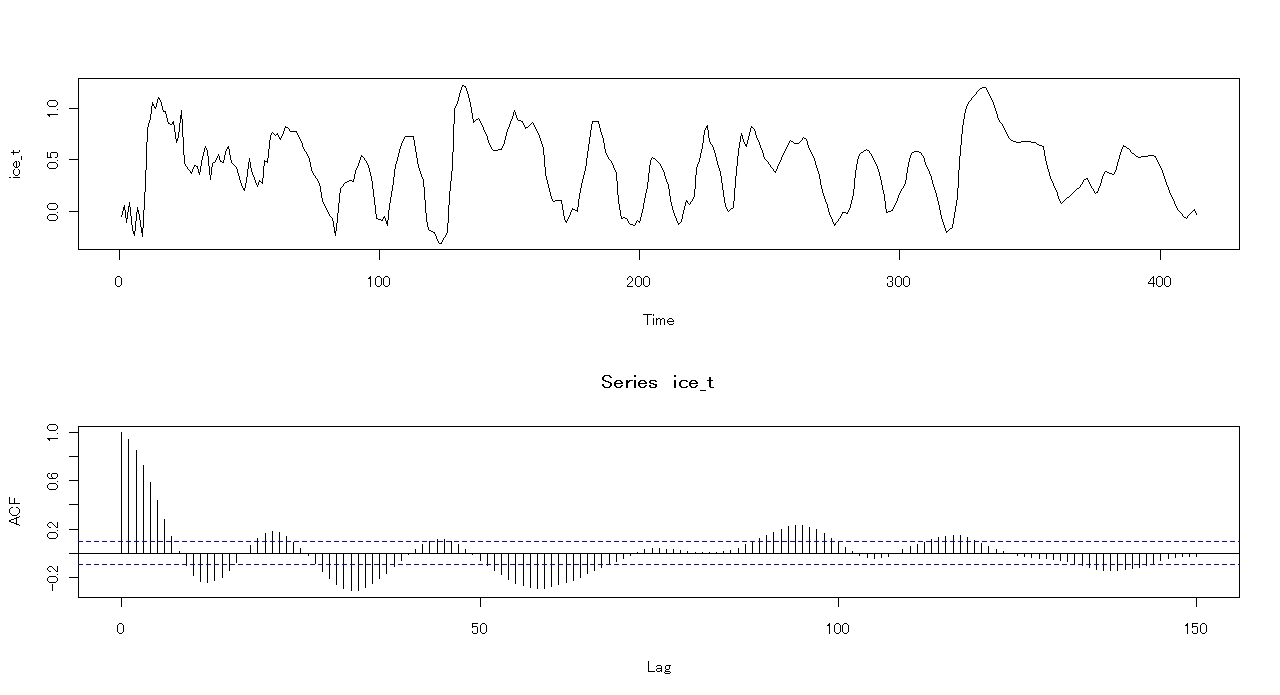
時系列を分割する

時系列の傾向が変わっていたら，そこで時系列を切ってみる方法があります．
Rではwindow() 関数よりこの作業がおこなえます．

ice_t1 <- window(ice_t,start = 1,end = 207)
ice_t2 <- window(ice_t,start = 208,end = 414)

時系列を真ん中で切って t1 と t2 に分けました．
この2つの時系列とそれぞれの自己相関を並べて表示していきます．

par(mfrow = c(2,2))
ts.plot(ice_t1)　　　　　　　　･･･1行1列目に表示
ts.plot(ice_t2)　　　　　　　　･･･1行2列目に表示
acf(ice_t1,lag.max=150)　　･･･2行1列目に表示
acf(ice_t2,lag.max=150)　　･･･2行2列目に表示

以上より次のように表示されます．

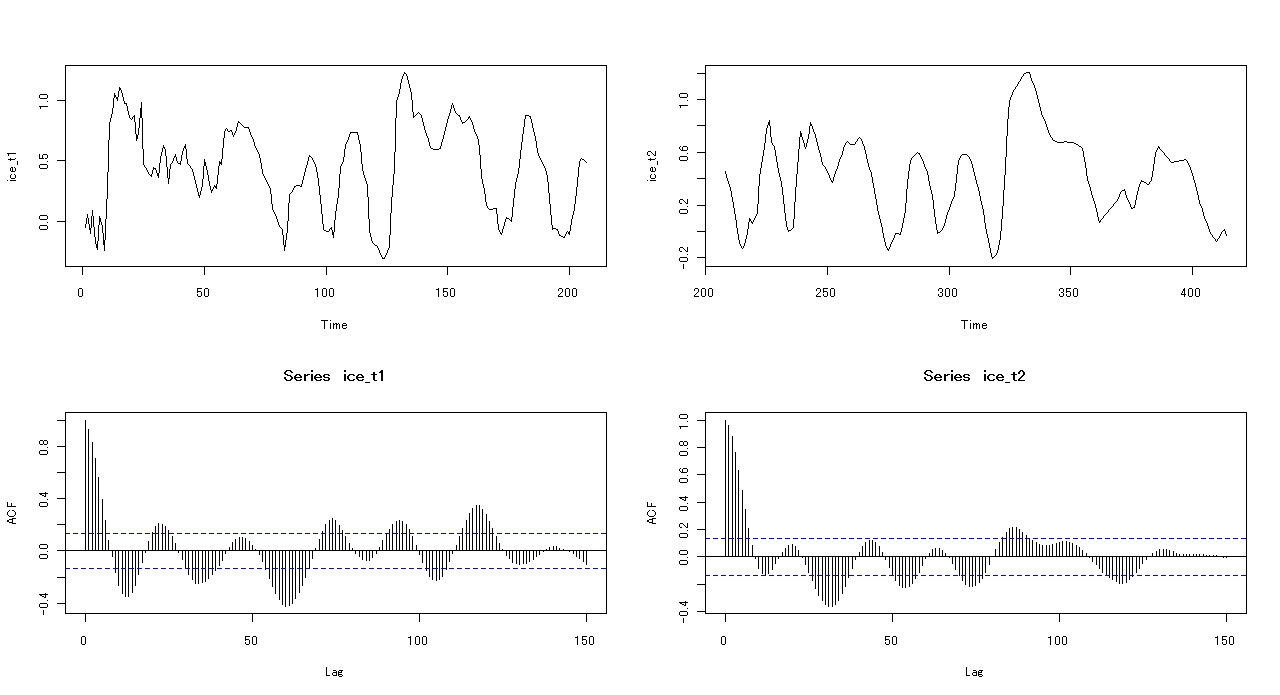
今回はここまでになります．保存するのを忘れずにRを終了させてください．

---