bluebikeleaf @ ウィキ
bluebikeleaf @ ウィキ

電子回路 > 発振回路 > コルピッツ発振回路

コルピッツ発振回路


コルピッツ発振回路について勉強してみました。下図１がコルピッツ発振回路の交流等価回路です。発振回路は、増幅回路と、出力の一部を入力に帰還する帰還回路によって構成されていると思います。でも、図1を見ても帰還回路の部分がよく分かりませんよね。



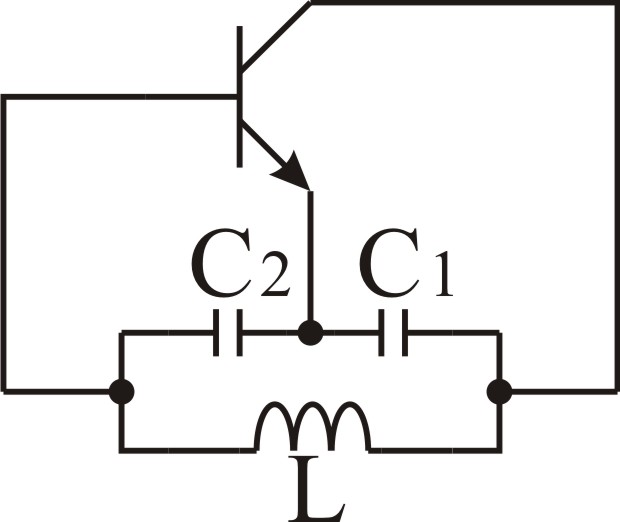
図１：コルピッツ発振回路

そこで、図２のように書き直すと帰還回路となっていることが分かると思います。



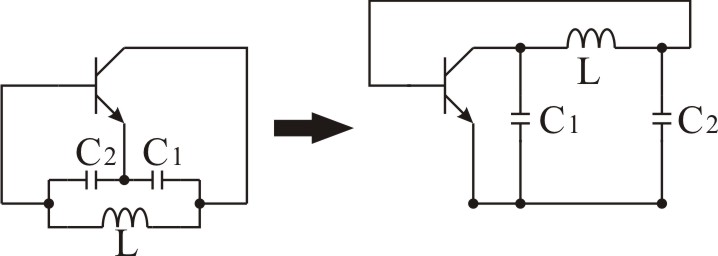
図２：書き直したコルピッツ発振回路

エミッタ接地のトランジスタ入力インピーダンスをZ(簡単のために実数とします)として、共振条件を求めてみたいと思います。図３のように、最初のベース電流をi_b、帰還回路を一巡したあとのベース電流をi_b'とおきます。\frac{i_b'}{i_b}を求めることで、共振条件を求めることができます。
未知数は、i_1, i_2, i, i_b'の4つです。



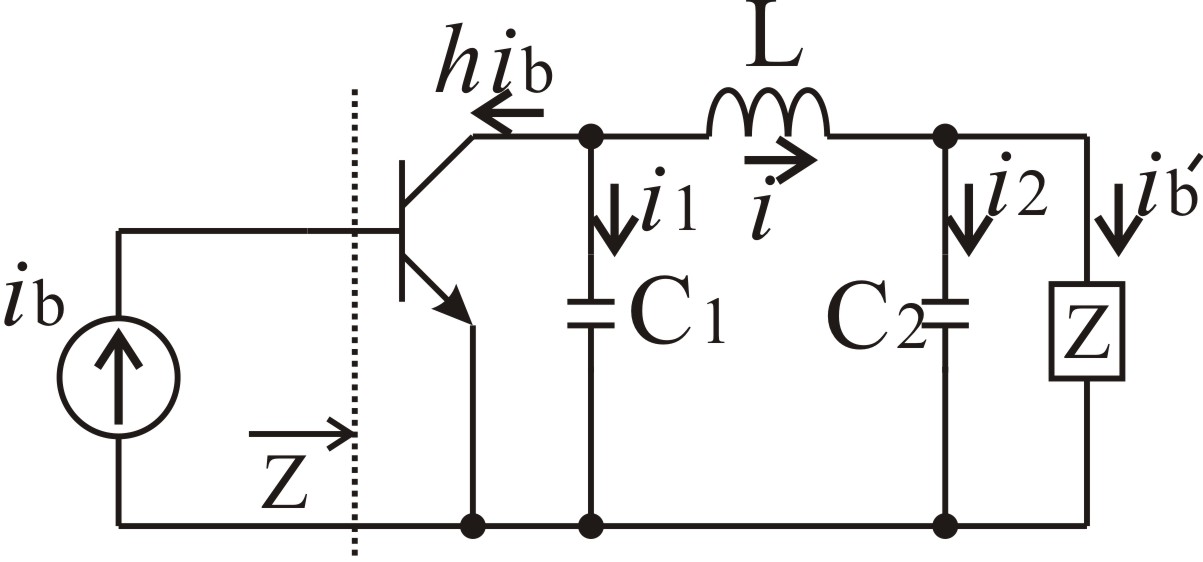
図3

キルヒホッフの電流則から

hi_{b} = i_{1}+i (1)
i = i_{2}+i_b' (2)

電圧則から

\frac{1}{j\omega C_1}i_1 = j\omega L i + i_b'Z (3)
\frac{1}{j\omega C_2}i_2=i_b'Z (4)

となります。未知数が4つで方程式も4つあるので、これらの方程式を連立して解くことでi_b'をi_bであらわすことができます。(1)～(4)式を解くと

\frac{i_b'}{i_b} = \frac{h}{(1-\omega ^2LC_1)+j\omega [-\omega ^2LC_1C_2+C_1+C_2 ]Z} (5)
が得られます。

電流が帰還回路を一巡したときに位相が同相となる周波数で回路は共振します。いいかえると、(5)式左辺が実数であるときi_bとi_b'が同相であるので、(5)式右辺の虚部が0となる周波数で回路は共振する。ということになります。

したがって、共振条件は
-\omega ^2LC_1C_2+C_1+C_2=0 (6)
となります。(6)式より共振周波数は、

\omega = \sqrt{ \frac{1}{L}\cdot \frac{C_1+C_2}{C_1C_2} } \equiv \sqrt{\frac{1}{LC}} (7)
となります。
ここで、CはC_1とC_2を直列接続したときの合成容量をあらわしています。


次に、発振するための利得条件を求めてみます。
電流が帰還回路を一巡したときに、その振幅が最初と同じかそれ以上となっていれば、発振すると思います。つまり、(5)式において、左辺の絶対値が1以上であることが利得条件になると思います。

|\frac{i_b'}{i_b}| \geq 1 (8)
(5)、(6)式より(8)式は

| \frac{h}{1-\omega ^2LC_1} | \geq 1 となります。

ここで、 (6)式より

1-\omega ^2LC_1 = 1-\frac{C_1+C_2}{C_2} = -\frac{C_1}{C_2} であることから、(8)式は

| \frac{h}{- \frac{C_1}{ C_2}} | \geq 1 \Leftrightarrow - \frac{h}{- \frac{C_1}{ C_2}} \geq 1 \Leftrightarrow h \geq \frac{C_1}{C_2} (9)
となります。(9)式が利得条件を表していると思います。

位相条件と利得条件をあわせて発振条件になります。
「コルピッツ発振回路」をウィキ内検索
最終更新：2008年08月06日 17:26
ツールボックス

下から選んでください:

新しいページを作成する
ヘルプ / FAQ もご覧ください。