bluebikeleaf @ ウィキ
bluebikeleaf @ ウィキ

電子回路 > 雑音 > 雑音指数

雑音指数


雑音指数について学習しました。



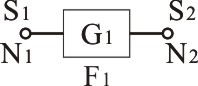
図１：雑音指数

雑音指数は、出力側のSNに対する入力側のSNの比を表しており、
F=\frac{S_1/N_1}{S_2/N_2}
ですが、入力雑音N_1は、N_1 \equiv kTBで定義されています。
ここで、kはボルツマン定数です。Bは雑音の帯域幅だと思います。

「雑音指数は入力雑音がN_1=kTBのときで評価される」ということを忘れていると、縦続接続した場合の雑音指数の計算方法が分からなくなってしまいます。

増幅器の利得をG_1とすると、図1の雑音指数は

F=\frac{S_1}{S_2}\cdot \frac{N_2}{N_1} = \frac{N_2}{G_1kTB}となります。

また、N_2=G_1N_1+N_{e1}=G_1kTB+N_{e1}と表すことができるとすると、

F=\frac{G_1kTB+N_{e1}}{G_1kTB} と表現できます。


縦続接続した場合の雑音指数




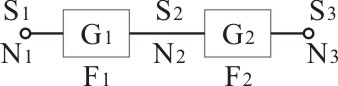
図2：2段縦続接続

図2のように、雑音指数がF_1、F_2の増幅器を縦続接続した場合のトータルの雑音指数を考えて見ます。

N_2=G_1N_1+N_{e1} 、 N_3=G_2N_2+N_{e2} とします。

雑音指数は、

F=\frac{S_1}{S_3}\cdot\frac{N_3}{N_1} =\frac{S_1}{G_2S_2}\cdot\frac{G_2N_2+N_{e2}}{N_1}=\frac{S_1}{S_2}\cdot\frac{N_2}{N_1}+\frac{S_1}{S_2} \cdot\frac{N_{e2}}{G_2N_1}

{} = \frac{G_1kTB+N_{e1}}{G_1kTB}+\frac{1}{G_1}\cdot\frac{G_2kTB+N_{e2}-G_2kTB}{G_2kTB}

=F_1+\frac{F_2-1}{G_1}

となります。


さらに、n段縦続接続した場合の雑音指数は、

F_{n} = F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1G_2}+\cdots + \frac{F_n-1}{G_1G_2\cdots G_{n-1}} \cdot \cdot \cdot \cdot \cdot \cdot (A)

となります。数学的帰納法を用いれば簡単に証明できます。
+ ...
(1) n=2のとき
先の計算より、 F_{2}=F_1+\frac{F_2-1}{G_1}と求まっており、n=2のとき(A)式は成り立つ。

(2) n=kのときに(A)式が成り立つと仮定する。すなわち



図3：k段縦続接続 


F_{k} = F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1G_2}+\cdots + \frac{F_k-1}{G_1G_2\cdots G_{k-1}}    \cdot \cdot \cdot \cdot \cdot \cdot (B)
が成り立つと仮定する。



図4：k+1段縦続接続

次に、図4のように(k+1)段縦続接続した場合の雑音指数を導出する。

N_{k+2}=G_{k+1}N_{k+1}+N_{e(k+1)} とする。

F_{k+1}=\frac{S_1}{S_{k+2}}\cdot\frac{N_{k+2}}{N_1}

=\frac{S_1}{G_{k+1}S_{k+1}}\cdot\frac{G_{k+1}N_{k+1}+N_{e(k+1)}}{N_1}

=\frac{S_1}{S_{k+1}}\cdot\frac{N_{k+1}}{N_1}+\frac{S_1}{S_{k+1}} \cdot\frac{N_{e(k+1)}}{G_{k+1}N_1}

{} = F_{k}+\frac{1}{G_1G_2\cdots G_k}\cdot\frac{G_{k+1}kTB+N_{e(k+1)}-G_{k+1}kTB}{G_{k+1}kTB}

= F_{k} + \frac{F_{k+1}-1}{G_1G_2\cdots G_k}

(B)より、

F_{k+1} = F_1 + \frac{F_2 - 1}{G_1} + \cdots + \frac{F_{k+1} - 1}{G_1G_2\cdots G_{k}}

が成り立つ。

以上より、n=kのときに(A)式を仮定した結果、n=k+1の場合にも(A)式が成り立つことが証明された。

(1)より、n=2のとき(A)式は成り立つ。(2)より、n=2のとき(A)式が成り立つのでn=3のときにも(A)式が成り立つ。引き続き(2)より、n=3のとき(A)式が成り立つのでn=4のときにも(A)式が成り立つ。\cdots

したがって(1)、(２)より、n\ge 2のすべての自然数nについて、(A)式が成り立つ。

証明終わり。
「雑音指数」をウィキ内検索
最終更新：2008年10月03日 17:12
ツールボックス

下から選んでください:

新しいページを作成する
ヘルプ / FAQ もご覧ください。