一陸技/基礎/ΔY変換の公式の導出 - bluebikeleaf @ ウィキ

一陸技 > 基礎 > ΔY変換の公式の導出

$\Delta - Y$ 変換の公式を四端子行列(Fマトリックス)を用いて導出します。

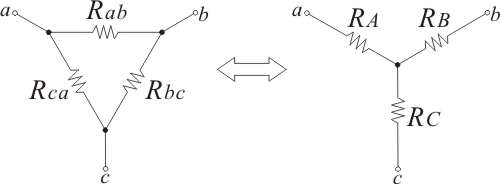
図１： $\Delta - Y$ 変換

図2に基本的な四端子回路の四端子行列を示します。

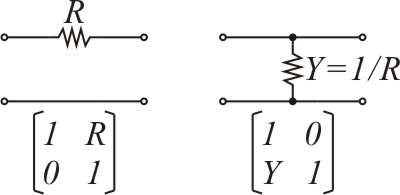
図2：四端子行列

この基本的な四端子回路を縦続接続していったときの四端子行列は、それぞれの行列を順番に掛け算していくことで機械的に求めることができます。 $\Delta$ 回路も $Y$ 回路も四端子回路で表現できます。図3に示します。左右の回路が等価であるとき、それぞれの四端子行列も等しくなります。

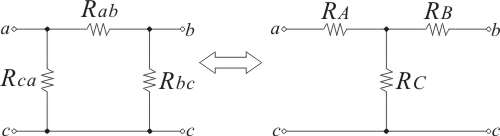
図3：四端子行列で表現するために書き直した $\Delta$ 回路と $Y$ 回路

$\huge \displaystyle \begin{bmatrix}1 & 0 \\ \frac{1}{R_{ca}} & 1 \end{bmatrix} \huge \displaystyle \begin{bmatrix}1 & R_{ab} \\ 0 & 1 \end{bmatrix} \huge \displaystyle \begin{bmatrix}1 & 0 \\ \frac{1}{R_{bc}} & 1 \end{bmatrix} = \huge \displaystyle \begin{bmatrix}1 & R_A \\ 0 & 1 \end{bmatrix} \begin{bmatrix}1 & 0 \\ \frac{1}{R_C} & 1 \end{bmatrix} \begin{bmatrix}1 & R_B \\ 0 & 1 \end{bmatrix}$

行列の掛け算を計算すると次のようになります。

$\huge \displaystyle \begin{bmatrix} 1+\frac{R_{ab}}{R_{bc}} & R_{ab} \\ \frac{R_{ab}+R_{bc}+R_{ca} }{R_{bc}R_{ca}} & \qquad 1+\frac{R_{ab}}{R_{ca}} \end{bmatrix} = \begin{bmatrix} 1+ \frac{R_A}{R_C} & \qquad \frac{R_AR_B+R_BR_C+R_CR_A}{R_C} \\ \frac{1}{R_C} & 1+\frac{R_B}{R_C} \end{bmatrix}$