再帰呼び出しと分割統治法

再帰呼び出し

再帰呼び出しとは読んで字のごとく、そのアルゴリズムの中で自分自身を呼び出しているようなアルゴリズムを言います。
といっても意味わからないと思うので典型的な例を挙げます。

階乗を求めるようなアルゴリズムを考えます。まあ単純にC言語ならばforループを回せば求められるけどもそういわずに。
Factoial(n)っていうアルゴリズムを作ります。再帰呼び出しを使った階乗のアルゴリズムの中身は簡単に

if n=1 then return n
else then return n*Factorial(n-1)

…さて、こういうアルゴリズムを考えていると自家撞着的で気持ち悪さを感じるかもしれません。
また、これぐらい単純だとそうは感じなかったかもしれませんが、次の問題ではどうでしょう。

マージソート

マージソートは再帰呼び出しを使ったソートの方法です。では実際に、n項からなる数列SをソートするアルゴリズムMERGESORT(S)を下に書いてみます。

if n=2 then return (min(S), max(S)) else
 begin
  Sを大きさの等しい二つの集合TとUに分解する。
  集合Tの成分←MERGESORT(T)
  集合Uの成分←MERGESORT(U)
  if  then ← else then ←
  … (この要領で、TとUの先頭から小さい順に取り出して集合Vを作る）
 return V

まあ意味わかんないですよね。
要するに要素の数が2じゃなければ、Sを2つの集合TとUに分割してそれをまたマージソートせえというわけです。つまり、再帰呼び出しです。

分割統治法

マージソートのプログラムをもう少し深く考えてみます。

昔懐かし（今もあるみたいですが）某カードゲームをやったことがある方は「チェーン」なんていうのを覚えているのではないでしょうか。
これも似たような考え方で、「アルゴリズムの中で再帰呼び出しが起こったらその時点で『そのアルゴリズムを一旦停止して』再帰呼び出しを行います。」
つまり、上のマージソートの

  集合Tの成分←MERGESORT(T)

この行でいったんこのプログラムを「ストップ！」して再帰呼び出しを行います。

この再帰呼び出しも、

  集合Tの成分←MERGESORT(T)

この行でやっぱり停止して再帰呼び出しに移ります。
じゃあこの連鎖はいつ終わるんでしょうか？というと、「n=2」となったときです。するとelse beginの中身にはいきませんから再帰呼び出しは発現しません。
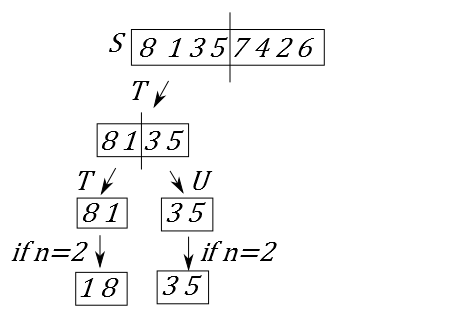
ここまでで起こったことを図にしてみます。

さて、こっからは上に登っていき止まっていたアルゴリズムを再起動させてやります。

次にこの行の処理をしてやります。

  if  then ← else then ←

上の図で言えば「Tの先頭から1をとる」「Uの先頭から3をとる」「Uの先頭から5をとる」「Tの先頭から8をとる」として「1358」を作り出すわけです。
その結果こんな感じになります。

まあこんな具合で繰り返しますと、次のような感じでソートが完了します。

この図を見ますと、『分割』して『統治』していますね。だからこんな方法を分割統治法と言います。