色を定量的にあらわす
色をデジタル的に操ろうと思えば、色もそれぞれちゃんと数値化してやらなければいけません。
このような色を数値の組を一対一で対応させる枠組みを表色系と言います。
表色系とは何か?
加法混色と減法混色の項でやりましたとおり、色は何らかの色を持った光を足していったり、白色光からある色を差っ引いたりして望みの色を作るのでした。
実はこの足していったり、差っ引いたりするような色の組み合わせですが、これらは3つの色を用意すれば大方任意の色が得られるといわれています。
これを
光の三原色と言います。
もうおなじみだと思いますがRGBというのはR、G、Bの3色を組み合わせて任意の色を作ろうという試みですね。
このようにある色が3原色のどのような混交で出来上がるかということを数値化したのが混色系と言われるものです。
RGB表色系
上で言った通りRとGとBで任意の色を表現するものです。これは加法混色の考えに基づいています。
CMY表色系
では白色光からRを差し引いた色とは何になるでしょう?これはシアンと呼ばれる色ですね。
このように白色光からある色を差し引いてやるとその色になるというような関係を補色の関係と言います。
他にもRGBの補色にはマゼンタとイエローがあります。
これらを使った表色系というのはCMY表色系と呼ばれています。
白色光から差っ引くという概念なので、減法混色の考え方ですね。
CIE-XYZ表色系
先ほどの項ではRGBはあたかもすべての色を再現できるような書き方をしましたが実情は違います。
(上記画像および以下の画像は
wikipediaから引用し改変したものです。)
このグラフはある単色光を実現するのにRGBをそれぞれどれだけ加えればいいか記述したものです。
例えば570nmの単色光と同じ色を作りたければRを0.17ぐらい、Gを0.19ぐらい入れれば良さそうですね。
もう気づいた方もいると思いますがこのグラフ、最大の問題点があります。
それは500nm付近の単色光を実現するのにRの「マイナス」の光を入れる必要があるということです。
光は波動です、波動にはマイナスという概念がありませんから実際にはRGBではこの領域の色を実現できないということになります。
(余談:そもそもこのマイナスってどうやって出てきたんだよ、ということを説明します。
色を扱う国際規格を作るCIEは実験によって次の事実を知りました。
『500nmの色+0.09のR=0.05のG+0.05のB』
つまり、-0.9の色を使って500nmに等色したというより、「500nmの色に0.9のRを加えることでやっとGとBを使って等色できた」ということです。
上の式を移行してやれば『500nmの色=-0.09のR+0.05のG+0.05のB』ですね。
つまりマイナスというのは表現の上での苦肉の策というか、あくまで形式的な表現にすぎません。)
さて、そこでCIEは任意の色を3色の正の値で作れるように、仮想的な色を考案しました。
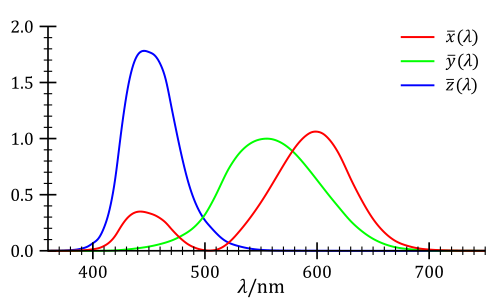
その仮想的な色の組はXYZと呼ばれるもので、そのXYZに基づけば単色光は次のグラフにしたがって等色できます。
最終更新:2012年11月16日 02:07