プロトタイプ法とは?
パターン認識の項でやった手順のうち(3)に当たるものですね。
例えばアルファベットの大文字Aか小文字aかどちらかに識別するような場合を考えてみましょう。
これらを特徴づける量として、例えば「角ばり具合(angular)」と「大きさ(big)」の軸で特徴空間を作ってみますと上みたいな図になります。
ここで、統計量の項でやった「中心」を表す量の「平均」「中央値」といった値をプロトタイプとしてそのクラスの代表値(図ではダイヤマーク)とし、新しく来た画像がどのプロトタイプに最も近い画像化によってクラスの判定を行うのがこのプロトタイプ法です。
最も"近い"とは?
実際の自然界において「近い」とは何か見たいな哲学的な問いを投げかけるつもりはありません。
ただ特徴として「近い」というのはどう評価したらいいのでしょうか?
一番素朴なのはやっぱり素朴な意味での距離、つまりユークリッド距離でしょう。
ユークリッド距離
新しい画像の特徴ベクトルが
![\vec{x}=[x_1, x_2,\cdots, x_n]^T](http://chart.apis.google.com/chart?cht=tx&chf=bg,s,ffffff00&chco=000000ff&chs=25&chl=%5Cvec%7Bx%7D%3D%5Bx_1%2C%20x_2%2C%5Ccdots%2C%20x_n%5D%5ET)
だったとしましょう。
この特徴ベクトルが

番目のクラスのプロトタイプ
![\vec{M_k}=[M_{k1},M_{k2},\cdots, M_{kn}]](http://chart.apis.google.com/chart?cht=tx&chf=bg,s,ffffff00&chco=000000ff&chs=25&chl=%5Cvec%7BM_k%7D%3D%5BM_%7Bk1%7D%2CM_%7Bk2%7D%2C%5Ccdots%2C%20M_%7Bkn%7D%5D)
からどれくらい離れているかは

というような二乗和で表せます。さて、この式、次のようにも表せるのは分かるでしょうか。

この式はベクトルとベクトルの掛け算ですが、縦ベクトルと横ベクトルの演算なので行列規則による積であることに注意してください。
マハラノビス距離
天下り的ですが、式(1)をこんな風に弄ってみます。


は

番目のクラスに属する特徴ベクトルたちの種々成分(つまり特徴量)同士の
分散共分散行列で

成分は
![E[(X_i-\mu_i)(X_j-\mu_j)]](http://chart.apis.google.com/chart?cht=tx&chf=bg,s,ffffff00&chco=000000ff&chs=25&chl=E%5B%28X_i-%5Cmu_i%29%28X_j-%5Cmu_j%29%5D)
であります。丁度ユークリッド距離の(1)式に分散共分散行列をサンドイッチさせたこの距離を
マハラノビス距離と言います。
さあ、式(2)には統計量が入ってきましたがこれはどのような働きをしているのでしょう。
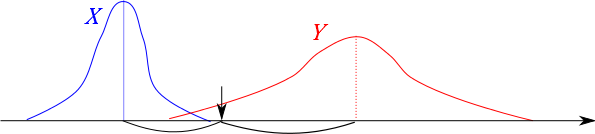
上の画像のような感じでそれぞれのクラスの特徴量が分布しているとします。
ここで「↓」のところの特徴量をもつ画像はどちらのクラスに分類されるべきでしょうか。
ユークリッド距離で言えば青色のプロトタイプの方が多少赤色のプロトタイプより近いです。
したがってユークリッド距離で言えば青が分類されるべきクラスになりますが・・・?
実際、青の分布は分散が小さいので「↓」のところの特徴量を持つようなサンプル画像はあまり存在していません。
対して赤色の分布は裾野が広いので、多少遠い「↓」の位置も完全に守備範囲に捉えています。
このように分類の上では、「それぞれのクラスの統計量」を考慮するとよりよい分類が出来ることがあり、その方法の一例がこのマハラノビス距離だということです。
javascript plugin Error : このプラグインで利用できない命令または文字列が入っています。
最終更新:2012年11月08日 01:13