主成分分析の画像情報処理における応用
パターン認識の手順(2)に値するとこの解説です。
上のページではアルファベットから丸みや大きさといった抽象量を用いて特徴空間を作りました。
このように人間の"感覚的な"概念によってある特徴を抽出するようなやり方を
ヒューリスティックスといいます。
しかし、「この図形は丸い」みたいなことは人間だからそういえるわけで、コンピューターには「丸い」なんて言葉は通じません。
そのため「どういうものが丸いと言えるのか」みたいなことを数値のようなものでちゃんと記さないといけないわけなのです。
ヒューリスティックスの難しさがお分かりになったでしょうか。
そこで、もう特徴云々言うのはめんどくさいから、「画素の値をそのまま使ってやろう」という風に考えるわけです。
例えば16×16のピクセルであれば256次元の特徴空間を使ってやればいいわけです。
つまりそれぞれグレースケールの画像だとして、明度を1個目のピクセル、2個目のピクセル、3個目のピクセル、

みたいに指定していくわけですね。
…こうすれば何も考えなくていいわけですがドット絵みたいな画像でもこれだけの次元がいるわけです。
そこで、この次元をもう少し落としてみようと考えるわけです。その手法が主成分分析というものです。
主成分分析の概念的理解
まずこの項の趣旨を思い出すと
「入力画像からそのクラスを特徴づけるような量(特徴量)を取り出す」
ということでした。
ではこの『特徴づけるような量』とはなんでしょうか?
パターン認識のページでは大文字のAと小文字のaを判別する、という例を考えました。
例えばこれ、特徴量を「色」として選んでみたらどうでしょう。
文字認識というのは基本的に、黒で書かれた文字を判別するのに使いますから、入力画像も全部黒にします。
この黒だらけの中で、あるクラスを特徴づける特徴量が「黒」とは・・・?
その人を判別する方法として適当なのは、その集団にあって皆が皆違うようなものが適当なはずです。
あるクラスの生徒を判別する方法であれば、顔・身長・声・性格・・・などはその「特徴」というにふさわしいですが
「年齢」みたいなものはせいぜい数か月程度しか変わらずに「特徴」というにはふさわしくないはずです。
長々と言ってきましたが、要するに言いたいことは
「特徴量としてふさわしいのは『分散が大きい』ような量」
ということです。
では実際に一番簡単な例として単純化して2次元の特徴空間(特徴平面)を1次元の特徴空間(特徴線?)に落とし込むことを考えましょう。
2次元を1次元にする方法は平面の点の、平面上の直線への射影ですよね。
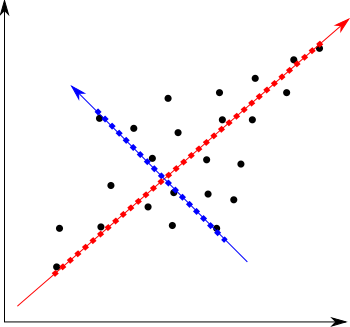
平面上の直線といえば例えば上の図で言えば赤の直線だったり青の直線だったり、また縦軸(y軸)や横軸(x軸)への射影でもいいですよね。
x軸への射影というのはそのまますべての点のx座標成分だけを抽出することになりますし、y軸への射影はy座標成分だけの抽出になります。
また赤の直線や青の直線みたいな直線の射影は、両方の成分を重みづけして抽出していることに等しいです。
今までの議論によれば特徴量としてふさわしいのは『分散が大きい』量です。
ですので射影をして次元を減らすにしても分散が大きくなるような射影直線を考えた方がよさそうですね。
それが上の図で言えば「赤の直線」です。このような直線への射影成分を第一主成分といいます。
一般次元の主成分分析
「第一」主成分ということは第二・第三もありそうですね。
一般

次元の特徴空間を

次元に落とす場合、
第2主成分、
第3主成分、…、第

主成分があるわけですが
まずは第二主成分を次のように決めます。
『第一主成分に直交している直線の中で、第一主成分の次に分散が大きくなるような射影直線』
このように第二主成分を決めて、第一主成分との張る平面を考えれば、ちゃんと特徴ベクトルの射影がが散らばるような2次元平面の特徴空間が出来上がるというわけです。
この『第一主成分に直交している直線の中で、第一主成分の次に分散が大きくなるような射影直線』っていうのはさっきの図で言えば青い直線になりますね。
まあ元が二次元の特徴空間なので第二主成分を考えても意味ないんですけど。次元を落とせませんからね。あくまで例です。
こんな感じで第

主成分を
『第

主成分と直交している直線の中で第

主成分の次に分散が大きくなるような射影直線』
として定義します。言うまでもないかもしれないですが第

次元の話なのでもはや幾何学的な意味での直線とかではないことに注意してくださいね。
主成分の具体的な求め方
ではいよいよ主成分の求め方を紹介します。この求め方はすごく簡単で
『第

主成分は分散共分散行列の
固有値が

番目に大きい
固有ベクトルと同じ方向に軸が向く』
ということらしいです。
つまり、ある

次元の特徴空間に分布する特徴量を

次元に圧縮したいのであれば
(1)
固有方程式を解いて固有値を求める。
(2)求めた固有値の中から

番目までに大きい固有値について、固有ベクトルを求める。
(3)それら固有ベクトルが張る空間

を求める。
(4)

次元空間の特徴ベクトルを(3)で求めた空間

に射影する。
という手順で出来てしまうわけです。
分散を扱うということで
分散共分散行列を取り出してきたわけですが、こんな簡単にその最大の分散方向が分かってしまうのですね。
最終更新:2012年11月08日 01:13