「明るさ」の3つの視点
人間が「明るさ」とか「色」とか、物理的に言えば「電磁波」を視覚的に観測する場合、その観測対象は二種類に分かれます。
それは、観測対象そのものが光っている(例えば太陽や蛍光灯)場合、もう一つは何か他の光を受けてその光を反射して色を発している場合、です。
前者のような光源から発せられる光の強さ、つまりエネルギーの事を放射束といい、単位はエネルギーなのでワット[W]になります。
これを立体角で割ったものを放射強度といいます。単位は[W/sr]ですね。(立体角については次の項を。)
後者の場合、光が辿るプロセスは次のようになります。
「光が光源から発せられる(放射束)」⇒「光がある物体に当たる」⇒「物体から光が反射されて観測者の目に届く」
ここで2つ目のプロセス、つまり物体側から光のエネルギー密度を
放射照度という指標で考えます。単位は[W/

]。
次に3つ目のプロセス、つまり物体から反射された光のエネルギー密度は
放射輝度という指標を使います。単位は[W/sr

]。
放射照度と放射輝度という2つの指標の違いは観測してる物体が「光を受けている」という見方をするか「光を発している」という見方をしているかの違いです。
同じだけの放射照度を受けていてもその物体が黒か白かによって放射輝度は変わってきますし
同じだけの明るさを観測したとしてもその物体が同じだけの光を受けているとは限りません。そこが放射照度と放射輝度の大きな違いです。
さて、大まかにイメージは以上になりますが、単位がごちゃごちゃとややこしいですね。
次の項にてそれら厳密な意味について詳しく検討していきます。
そもそも立体角とは
ざっくり立体角がどんなものか言ってしまうと、『ある視点からあるモノを見たときの見かけ上の大きさ』です。
もう少し詳しく説明しましょう。
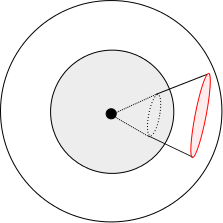
この図、半径

の球の中に半径1の球があるような状況を表しています。半径1の球は図の灰色の部分です。
ここで半径

の大きい球の表面上に赤色で表されている部分の面積があります。
この面積は

が大きくなるほどに大きくなるのは分かりますでしょうか?
球の表面積全体は

ですから、その中の例えば赤い面積の部分が全表面積の3%だったとしたら

つまり、定数

倍掛ける半径の二乗ですので、半径の二乗に比例して赤色の面積は大きくなります。
ある面積の立体角とはこの

の値を指します。
つまり、ある面積というのは「立体角×原点からの距離の2乗」という風に考えられるわけです。
ここで、文字通り別の見方をしてみましょう。あなたが原点から、さっきの図で言う赤色の面積を見ているとします。
まあいうまでもなくこう見えます。立体角は言い換えれば(SI単位系で言えば)
『1m先にコイツを覆い隠すための黒い紙を置きたい。そのために必要な紙の面積』(

に

を代入すれば面積=立体角)
赤い面積が1mより遥か遠くにある場合、必要な紙の面積は赤い面積よりは小さくていいことが、遠近法的に分かるでしょう。
さきほど「見え方」と言ったのはそういうことです。
同じ面積を見ていても、遠くにある面積の方が小さく見える。つまり覆い隠すのに必要な面積は小さくなる。
遥か遠くにある山ならB4の紙とかですっぽり覆い尽くせてしまう、本当はものすごく大きいのに。
これが立体角のココロです。
さて、先ほど「面積=立体角×原点からのの距離」だと言いました。ここで言う面積とは「実際の面積」です。
これを式変形してやると「立体角=面積÷原点からの距離の二乗」となり、つまり
『ある面積の見え方は原点からの距離の二乗に反比例する』
ということを意味しています。
ちゃんと立体角を定義
もう一回この図に戻りましょうか。
どうしたらこの赤い面積を覆い尽くせるか。感覚的に点線で描かれた丸の部分のとこに黒い紙を置けばよさそうです。
つまり、『ある面積の、半径1の球への射影』が立体角だということもできます。
さらに数学的に正確に言えば、
『面積を構成する点と原点を結んだ直線

があったとする。この

のうち、原点から1の距離に位置する点の集合が立体角である。』
立体角で割ることの意味
放射束の定義は「全放射エネルギー÷立体角」でした。
別に「÷面積」とかにしてくれれば新しく立体角なんて勉強しなくてもいいのに。
しかしこれを使った方がより『太陽』の目線に立って考えられるのです。
例えば『

[W/

]だけ太陽が光を放射している』という文言があったとします。
メートル二乗で割っていますのでこれは「÷面積」の考え方ですね。
すごく単純に考えれば

が大きければ大きいほど太陽が強く輝いているといえます。しかし話は本当にそう単純でしょうか?
これ、『どこにその面積を置いているか』によって全然値が変わってきます。
同じ

でもものすごく間近で測っているか、遠くで測っているかで全然光の量が違いますから。
立体角にするとこういう問題は起こりません。
全て光源を原点とする半径1の円上で議論することができますから、遠いとか近いとかそんなことは考えなくてもよいのです。
さて、ここまでは放射強度の話でしたが同様に照度や輝度についても考えていきましょう。
照度が面積割りなのは、それが光を受けている物体目線での光量だからです。遠ければ遠いほど受ける光量は小さくなければいけませんから、立体角で割ってはいけませんね。
輝度が面積と立体角両方で割っているのは、輝度の正確な定義が以下のようになるからです。
『単位面積あたりの物体が発している光量』
まず、ある物体が発している光の量を考えているので立体角で割るのはいいと思います。光を発している側目線ですから。
次に面積で割る理由ですが、この面積というのは「光を受けている側」の面積ではなくて「光を発している側」の面積です。
基本的に光源は「点」が普通であると考えていますので、面積も糞も無いんですが、反射している方の物体はちゃんと大きさを持った量を想定していますからね。
ある単位面積の物体から反射した光でその光量を評価しようというわけです。
光に関する単位
このあたりの単位はすごくごちゃごちゃしますね。色々な本やここを含め色々なサイトを読み返してみてゆっくり理解してください。
上では

という単位を基準にしましたが、それぞれ別の表し方があります。
放射束に関して、これはジュールではなく
ルーメンをつかうことがあります。記号はlmです。
放射強度、つまりルーメンのsr割りは
カンデラという単位も使えます。これはcdという記号であらわされ、SI基本単位にも数えられます。
照度はルーメンパーメートル二乗でもいいですが、
ルクスという単位も使えます。記号はlxです。勉強机とかによく使われる単位ですね。
照度に関する法則
照度、つまりある物体に当たる光の量、に関する法則を二つ紹介しましょう。
長くなるので証明はしませんが、立体角

とある面積

の関係は次のようになります。

距離の2乗に反比例することはいいですね。
この式の

ですけど、これは当たっている平面の法線ベクトルと、光線の方向ベクトルのなす角を表しています。
これは太陽が上から照っている場合より、斜めから照っている方が暗く見える、ということから理解できます。
これらの法則には名前が付いています。
距離に関する法則は照度の逆二乗則、方向に関する法則は照度の入射角余弦則と言います。
javascript plugin Error : このプラグインで利用できない命令または文字列が入っています。
最終更新:2012年11月10日 21:03