メディア情報処理
メディア情報処理

2値化

2値化とは？

2値化というのは読んで字の如し、画像を２つの値のみで表そうというものです。
へそ曲がりでなければこの２値は黒と白ですね。
ですので、元の画像を黒と白の二つの画像だけで表現してやろうというのがこの2値化です。

じゃあ黒と白ってまずなんだろうということですが、これはRGBでいえばR,G,Bが「すべて0」か「すべて255」のモノを指します。
文字なんかは基本的に黒と白で表されていますけども、実際文字と背景の境界などはもう少し濃淡がなめらかに繋がっているはずです。
この色は「RとGとBの値がすべて一致している色」、つまりグレーですね。
いきなりカラー画像を黒と白だけにしてしまうのは飛びすぎなので、まずはこのグレーだけを使った画像（グレースケール）に直して使います。

ちなみにこのグレースケール、『色』の情報量が1次元になっているのはお分かりでしょうか？
普通色はRGBなど3つの数で指定されますが、グレースケールはすべての成分が同じだと言ってるので一つの数を用意すれば済むわけです。

そこで2値化とは、ある閾値（スレッショルド）を持ってきて、その閾値以上の色を白、それ以下の色を黒とするわけです。
例えば閾値を120に設定したら、「60,60,60」の色は「0,0,0」に、「130,130,130」の色は「255,255,255」に変換されるわけです。

ところで例えばスレッショルド10とかにしてしまったら、なんか真っ白けの画像になってしまいますね。「11,11,11」の色も全部「255,255,255」の白になってしまうのですから。
そういうわけでこの閾値を決める決定方法というのは非常に重要になります。
では以下で色々なスレッショルドの決め方について紹介していきましょう。

p-タイル法

p-タイル法とはいわば定員が決まっている入試みたいなものです。

例えばある画像がすでに「黒の量はこのぐらいが最適」と分かっていたとします。
そのような基準があるならば、その最適値に合わせて黒を「採用」してやればいいのです。

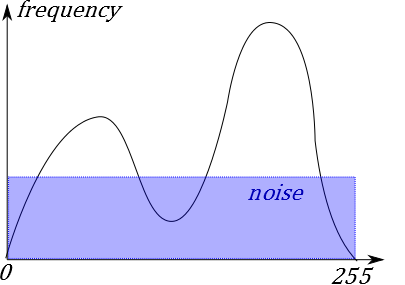
具体的に下図のような画素値の頻度分布になったとします。（frequencyは周波数じゃなくて『度数』の意なので注意。）
このような場合なら左から積算して行って、積算結果が所望の最適値になった時点をスレッショルドとしてやればいいのです。
そうすれば求める黒の量を持った2値化が出来上がります。

と、これは単純ですが最適値が手に入る手法です。
しかし問題点は、その『最適』がどこか分からないときです。
例えば初めからその画像が『い』というひらがなを表していて、それを二値化するならば『い』に含まれうる黒の量を最適値とすればよいのですが
汎用性のOCRなど、どんな画像が入ってくるか分からないにも関わらず、『い』と同じ感覚で、例えば『龍』という文字を二値化してしまったら・・・
なんかスッカスカの『龍』が誕生してしまいそうですよね。漢字が必要とする黒の量はひらがなより大きいのです。

モード法

じゃあもう少し一般的な方法を考えてみましょう。

さっき何気なく提示した頻度分布ですが、これは経験的に、一般の『文章』においても当てはまる図なのです。
特徴としては双子山ですね。
この双子山の左の部分が黒、つまり文字を表していて、右の部分が背景というわけです。

このような経験的知識（ヒューリスティックス）を用いて分別する方法をモード法といいます。
ただしこの双子山の谷、ノイズの海に埋もれてしまうような状況があるのでそう言った場合には工夫が必要になります。

判別分析法

判別分析法は統計的にスレッショルドの画像を決めてやろうという手法です。
まず画像全体について、その平均、標準偏差、要素数を\mu_t,\ \sigma_t,\ \omega_tと定義しておきます。

次にあるしきい値を用意できたと仮定して、「黒」に分類されたクラスを1、「白」に分類されたクラスを2とします。
そして、黒のクラスの平均、標準偏差、要素数を\mu_1,\ \sigma_1,\ \omega_1と定義します。
白のクラスについても同様に\mu_2,\ \sigma_2,\ \omega_2と定義します。

まだまだ定義が続きます。次にクラス間分散\sigma_b^2を次のように定義します。
\sigma_b^2=\frac{\omega_1}{\omega_t}(\mu_1-\mu_t)^2+\frac{\omega_2}{\omega_t}(\mu_2-\mu_t)^2
式の意味は大丈夫でしょうか？つまり平均のユークリッド距離（の二乗）に、その要素数に応じて重みづけ平均をとったものがクラス間分散です。

さらにクラス内分散\sigma_w^2は次のように定義します。
\frac{\omega_1}{\omega_t}\sigma_1^2+\frac{\omega_2}{\omega_t}\sigma_2^2
単純にそれぞれのクラスの分散を要素数に応じて重みづけ平均したものです。

式変形で簡単に証明できる結果として次のような関係式があります。
\sigma_t^2=\sigma_b^2+\sigma_w^2 \cdots(1)
つまり、全分散はクラス内とクラス間の分散の和で表せるということです。

色々定義していましたがいよいよ本題。ではどんなクラスの分け方をするのが一番良いのでしょう？
まずその指標の一つが「クラス間分離」が大きい事です。
クラス間分散が大きいということは『クラス同士が上手い具合に離れている』ことを意味していますから。
もう一つは「クラス内分散」が小さい事です。
クラス内分散が小さいほど頻度分布が先鋭化していて、判別がくっきりつくからです。

両方を総合的に検討する指標として、次の分離度を定義します。
\frac{\sigma_b^2}{\sigma_w^2} = \frac{\sigma_b^2}{\sigma_t^2-\sigma_b^2}
等式は式(1)により成り立ちます。

ここで、ある画像を読み取っているとき、全分散は定数になりますね。
対して\sigma_b^2というのはそのクラスの作り方（つまりスレッショルドの設定の仕方）によって異なります。
したがって、分離度を大きくするには、クラス間分散\sigma_b^2を大きくするようにしきい値決定をしてやればいいことが分かります。


javascript plugin Error : このプラグインで利用できない命令または文字列が入っています。
「2値化」をウィキ内検索
最終更新：2012年11月12日 19:47
ツールボックス

下から選んでください:

新しいページを作成する
ヘルプ / FAQ もご覧ください。