領域分割処理
ある写真なんかをとった時、その画像には色んな物体が映っていますね。
ビルだとか、木だとか、人だとか・・・
これらのモノを画像から自動的に解析して、ある一つの領域として分割する方法を考えてみましょう。
領域統合法
一番単純な方法は、「近傍の中で最も画素値が近いものを統合」する処理を何度も繰り返すことです。
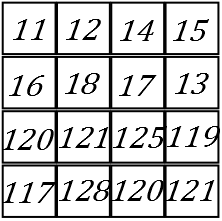
例えば画素値が
みたいな画素値を持つ3×3のビット画像があったとします。
ここで右下の画素を平均とって統合してやると
こんなことを繰り返していくと徐々に画像が平坦化していって最後は全画像が同じ画素値になってしまいます。
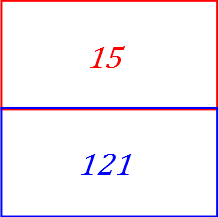
そうならない程度に平均化を止めると例えばこんな風になります。
これによって上の領域と、下の領域に領域分割が出来ました。
特徴量によるクラス分け
別の方法として
パターン認識という手法によるクラス分け方法があります。
ある物体領域がどのクラスに置かれるかというデータベースをもとに領域分割をするわけです。
スネーク
もう一つ、
スネークという手法は閉曲線のエネルギーを次のように定め、それを最小化することによりエッジを決定するような方法です。


は

を媒介変数とする曲線です。これら各項についてそれぞれ検討してみましょう。
まず、

について、より細かく分割すると次のようになります。

係数はそれぞれ重みづけの係数でその時々に応じて決定します。
さて、それぞれのエネルギーは


ここで、1個目の式ですが、これを式(1)にしたがって積分すれば、この曲線の『長さ』が出ますね。
二個目の式はまず曲線を微分しているので『方向ベクトルの向き』を表し、その微分を式(1)で積分しているので『方向ベクトルの向きの変位』を表しています。
つまり、曲線のなめらかさですね。
次に、

について、次のような式になります。

で表されます。ここで

は位置

における画素値を表しています。
ラプラシアンは全方向の周囲との値の差でしたね。
すなわちこの式は周りの画素値との差の"マイナス"ですから、エッジが強ければ強いほど小さな値になります。
以上のことを総合すれば
『曲線が短く』『曲線がなめらかで』『エッジが強い』ような曲線が境界として選ばれることが分かります。
javascript plugin Error : このプラグインで利用できない命令または文字列が入っています。
最終更新:2012年11月15日 22:53