R初心者のためのR操作ゼミ
このゼミでは、Rのまったくの初心者が、ある程度Rを使ってデータを見ることができるようになることを目的とします。
このページでは、データを取った後に研究者が行うと思われる手順をRで実行する方法について解説します。より詳細な技術については、以下のページをご覧下さい。
昔のゼミ資料
2008年4月8日からのアクセス数: -
目次
導入〜さあ、データをRで解析しよう!
題材
このページでは、森林の動態を研究している大学院生Aさんがデータを解析する道のりを見ていきます。Aさんはいくつかの固定プロットで立木の生残、樹種、サイズ(胸高直径)を測定しており、立木の生残動態を解析したいと思っています。
さて、Aさんは過去のデータを含め、2002年から2010年までの10000個のデータを収集しました。ここから、このデータをRを使って解析していきます。
使うデータ
下準備
Rの導入
まずはRを入手しないと始まりません。Rはインターネット経由で入手できます。
Windowsの方
CRANのページ から最新版のRを入手します。
.exeファイルをダウンロードし、アイコンをダブルクリックします。
インストールする途中で、インストールするコンポーネントを選択するところがあるので、「全てインストール」を選択します。
「起動時オプション」は「はい」にして、カスタマイズします。「表示モード」はSDIに、「ヘルプの表示方法」は「テキスト形式」に変更してください。あとはそのまま進んでください。
最初にRを起動したときに、文字が化けていることがあります。この場合、Rの上にある「編集」→「GUIプリファレンス」とたどると、新しくウィンドウが表示されます。ここの「Font」を「MS Gothic」に変え、下のほうの「適用」をクリックした後、「保存」をクリックしてください(ファイルネームは初期値のRconsoleそのままでいいです)。保存場所は、最初に表示されるフォルダにそのまま保存してください。
Windows Vistaの方で、上記のRconsoleがRの作業フォルダに直接保存できない場合、一度デスクトップに保存し、手動でRconsoleをRの作業フォルダに移してください。 データファイルの作り方
次に、取ったデータをなにかファイルに打ち込む必要があります。Rでは様々な形式のデータが読めますが、csv(ゑくせるにうちこんで、保存するときに選べる形式)がもっともトラブルが少なく、使いやすい形式です。
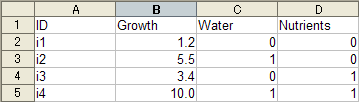
データを打ち込むときは、できるだけ各要素ごとに縦方向に並べる。
よい例
駄目な例(ゑくせらーにすごくありがちな形)
ゑくせるなどにデータを打ち込む。
各列に個体番号、環境条件などを入れる。
1 行目にはデータのラベルを入力する。
日本語、特殊文字(% や○×など)は絶対に使わない 。入力していいのは、数字、半角英文字のみ(生残なら0 と1 で区別する)。
基本的に空のセルを作らない。欠損値は、NAを入力しておく。
違った形式(並べ方が異なる)のデータを同一ファイル内に混在させない。 作ったデータの置き場
基本的にはどこでもいいです。ただ、トラブルが起きる確率を最小限にするのであれば、日本語やスペースなどが入っているフォルダの下には置かないで下さい。
Windowsの方:Rを起動して、「ファイル」→「ディレクトリの変更」と進んで、そのファイルがあるフォルダを指定します。
Macの方:Rを起動して、「その他」→「作業ディレクトリの変更」と進んで、ファイルがあるフォルダを指定します。 Rでのデータ操作
Rへのデータの読み込ませ方
Rを起動すると、
>
という状態になっていると思います。これはRが、「命令を出してください(準備オッケーです)」といっている状態です。
Rでは、マウスでかちかちしてデータを読み込んだりすることはできません 。この状態で、「ファイルを読み込んで」「図を作って」といった、コマンドを打ち込んで動作させます。ちょっと古いパソコンみたいですね。慣れないとしんどいと思いますが、頑張りましょう。
今回は、こちらで用意したbase.csvを読み込みます。
データを読み込むためのコマンド
で、以下のように入力します。
> d <- read.csv("base.csv")
これで、dという文字に、data.csvのデータをくっつけました 。このあと、何も文句を言われなかったら、
> d
と入力してみて下さい。base.csvのデータが表示されるはずです。
dという文字は、別にどんな名前でもよい。この、適当な文字列を、Rでは、「オブジェクト 」と呼ぶ。
Rでは、オブジェクトにデータをくっつけて作業をする。
オブジェクトの名前は自分で好きに決めることができるが、数字が最初に来る名前は付けられない(だめな例:0704iijima)。
read.csv("")は、csv形式のファイルを読み込みなさい、という命令である。
逆にここで文句を言われてしまった人は、以下の3点を確認してみて下さい。
打ち込んだスペルはあっているか?
データ(base.csv)のある場所が、Rにちゃんと指定されていない。ディレクトリの変更で、ちゃんとbase.csvがある場所を指定しているか?
日本語が入力できる状態で入力していないか(例えば<-は半角の<と-を続けて書くことで書いているが、日本語モードで変換して半角の<を出していないか)?Rでは半角英数文字しか受け付けない。 コピペでデータを読み込む方法(データファイルを作りたくない人)
データを読み込む方法として、直接データファイルを読み込まない方法もあります。
ゑくせるなどの上で、データの必要な範囲だけ選択してコピーします。そして、
> df <- read.table("clipboard")
とすれば、コピーした範囲が読み込まれます。
細かい注意点
上で見たように、Rではコマンドを打ち込んで動作させます。この後、どんどん複雑なコマンドが必要になってきます。そのため、Rに直接コマンドを打ち込むのではなく、メモ帳やWordなどに必ずコマンドを下書きし、Rにコピペして命令を出すようにして下さい 。
:を使うと、1ずつ変化する数列(等差数列)を生成できます。例えば、1:10と打ち込むと、1から10までの数列が生成されます。いろんな所で使うので、覚えておきましょう。 データの概要をつかむ
とりあえずデータを読み込むことには成功したAさんですが、データの数が多いので、このままではどんなデータになっているのかもよくわかりません。そこで、まずざっとデータの形や様子などを見る方法を紹介します。
使う関数
head():データフレームの上6行を取り出す。下6行についてはtail()。取り出す行数は、引数で調整可能。
nrow():データの行数を出してくれる。列数についてはncol()。
summary():各列の基礎的な統計量を出力。いろんな所で使う関数。
pairs():列同士の散布図を出力。 データの先頭を見る
> head(d)
Plot Sp DBH02 DBH04 DBH06 DBH08 DBH10
1 PlotA Sp56 14.773116 16.737987 19.31643 24.61452 NA
2 PlotA Sp46 10.959117 13.831113 17.40913 23.60213 30.27258
3 PlotA Sp60 6.136076 7.385640 NA NA NA
4 PlotA Sp35 17.835907 18.786075 22.41280 NA NA
5 PlotA Sp12 6.786937 8.408327 10.81423 14.00716 17.75146
6 PlotA Sp03 16.309994 20.569902 27.04936 35.76303 43.93186
こうすると、おおよそどのようなデータか視覚的に理解できます。
Plot:調査プロット名
Sp:樹種
DBH02:2002年の胸高直径。
DBH04:2004年の胸高直径。死亡した個体にはNAが入力されている。以下同様 データの数の調べ方
> nrow(d) #行数
[1] 10000
> ncol(d) #列数
[1] 7
各列の要約統計量
各列について、おおよそどの程度の範囲の値が入っているのかを見るには、以下のようにします。
> summary(d)
Plot Sp DBH02 DBH04
PlotP : 453 Sp57 :1206 Min. : 3.000 Min. : 3.943
PlotQ : 453 Sp26 : 934 1st Qu.: 6.904 1st Qu.: 8.968
PlotK : 448 Sp07 : 564 Median : 9.942 Median : 13.007
PlotV : 445 Sp12 : 521 Mean : 12.868 Mean : 16.712
PlotS : 443 Sp21 : 513 3rd Qu.: 15.458 3rd Qu.: 20.085
PlotD : 432 Sp56 : 488 Max. :162.271 Max. : 181.787
(Other):7326 (Other):5774 NA's :4000.000
DBH06 DBH08 DBH10
Min. : 5.118 Min. : 6.743 Min. : 8.68
1st Qu.: 11.981 1st Qu.: 15.805 1st Qu.: 20.69
Median : 17.344 Median : 22.754 Median : 29.24
Mean : 21.817 Mean : 27.811 Mean : 34.99
3rd Qu.: 26.531 3rd Qu.: 34.262 3rd Qu.: 43.04
Max. : 202.500 Max. : 224.257 Max. : 247.00
NA's :5294.000 NA's :5762.000 NA's :5999.00
データの関係を散布図で見る
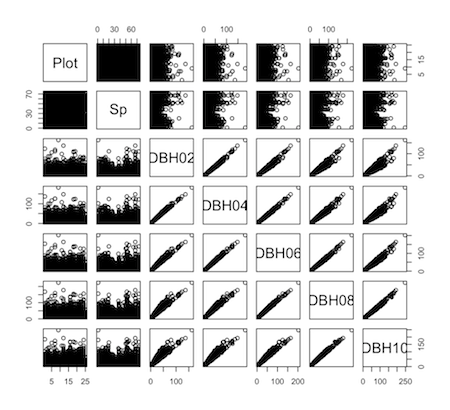
先ほどのsummary()は数字でしたが、列間の関係を視覚的に簡単に見るには、pairs()を使います。
> pairs(d)
データの部分的な抽出
データの概要がつかめたところで、A さんは今度は、「ある種だけのデータを見たい」「DBH が 10cm 以上のデータだけ見たい」といったような、データの一部だけを見たいと思い始めました。データの一部だけを取り出すために、この小節では以下の関数を使います。
データフレーム[行, 列]:行や列に当たる部分に、数字、列や行の名前、条件式などを入れて、それに従う部分だけを取り出す(とても重要!)
データフレーム$列名:特定の列を取り出す。
split():データフレームを、あるカテゴリーを示す列ごとに分割する。ゑくせるで言うところのオートフィルタに近い。
colnames():データフレームの列名を取り出す。仲間にrownames()。
plot():いわゆる散布図を描く。2編量感の関係を見るのに便利。
xyplot():同じく散布図だが、カテゴリーごとの図を作るのに便利。library(lattice)で呼び出す。 データの部分抽出
データの部分抽出は、Rの至る所で使うとても大事な操作です。繰り返し使って慣れましょう。
特定の列を取り出す場合は、列名や列の左からの番号などで取り出します。
> d[, 1] #1列目だけが取り出される
> d$Plot #列名を指定した場合
> d[, "Plot"] #これでも同じ
列を削除する場合は、列の番号にマイナスをつけるか、NULLを代入します。
> d[, -1] #1列目だけが抜けている
> d$DBH02 <- NULL
> head(d) #DBH02が削除されている
> d <- read.csv("base.csv") #元に戻す
列を加える場合は、新しい列名に入るデータを代入します。
> d$newdata <- d$DBH02 * 2 #DBH02を2倍したデータ
> head(d) #データが増えている
> d$newdata <- NULL #いらないんで削除
特定の条件でデータを取り出す場合は、以下のようにします。
> d[d$DBH02 >= 50, ] #DBHが50cm以上の個体のみを取り出す
> d[d$Sp == "Sp04", ] #SpがSp04のみ取り出す
最後の2つの例については補足します。まず、データフレーム[条件式, ]の形になっています。
条件式については、最初の例を取り上げます。d$DBH02 >= 50となっています。この結果、何が起こっているのでしょうか?こういう時は実際に打ち込んでみるとわかりやすいです。
> d$DBH02 >= 50
[1] FALSE FALSE FALSE
(以下略)
このように、DBH02が50未満の所はFALSE、以上の所についてはTRUEが入っています。
そして大事なのが、データフレーム[条件式, ]という書き方をしたときに、条件式の所にTRUEが入っている行は取り出され、FALSEが入っているところは取り出されない ということです。これを利用し、DBH02が50以上のデータだけを取り出すことができます。
条件式の書き方
ここで少し脇道にそれますが、条件式の書き方をまとめておきます。
a == b:aとbは等しい
a != b:aとbは等しくない
a > b:aはbより大きい
a >= b:aはb以上
a < b:aはbより小さい
a <= b:aはb以下
a | b:aまたはb
a & b:aおよびb カテゴリーごとにデータを分割
カテゴリーごとにデータを取り出す場合、ある 1つを取り出すなら上記の方法でいいですが、いくつかのカテゴリーのデータが欲しくなると、1つ1つ指定して取り出すのは面倒になってきます。その場合に、以下の関数を走らせるとカテゴリーごとにデータを分割できます。
> d2 <- split(d, d$Sp)
> d2[[3]] #Sp03のデータだけが取り出されている
> d2[["Sp03"]] #同じことを、カテゴリー名で
split()でデータを分割すると、カテゴリーの順番を示す数字、またはカテゴリー名でデータを取り出すことができます。
行・列名の取り出し方
データが大きくなると、とりあえず列や行の名前だけ取り出したくなることもあります。その場合は、以下のようにします。
> colnames(d) #列名
取り出したデータの視覚化
徐々に一部のデータを取り出せるようになってきたAさんですが、「取り出せても、数字だけ見てるんじゃよくわからないよなー」と思い始めました。そうしたときは図にしてみるのが一番です。ここでは、簡単な図の書き方を説明します。
2変量とも連続数の場合。
> plot(DBH04 ~ DBH02, d) #y ~ xという関係。
#Sp3だけに限定した図
> plot(DBH04 ~ DBH02, d2[[3]]) #先ほどのsplit()の結果を利用して
ちなみに、多くの作図や統計関数では、(y ~ x, データフレーム名)という書き方をします。覚えておいて下さい。
2変量の内1つがカテゴリー変数の場合。
> boxplot(DBH02 ~ Plot, d)
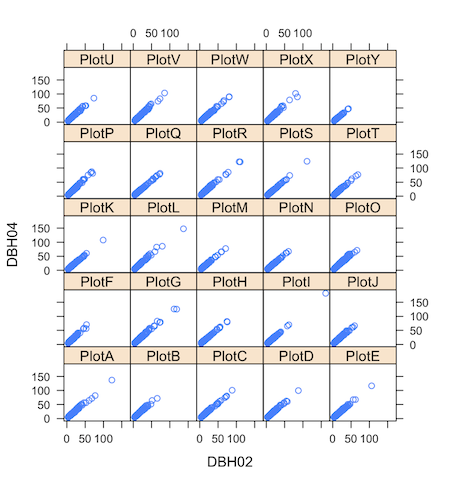
ちなみに、先ほどの散布図を何かのカテゴリーごとに描きたい(例えばPlotごととか)場合は、latticeパッケージのxyplot()を使います。
> library(lattice)
> xyplot(DBH04 ~ DBH02 | Plot, d) #|の後ろに、カテゴリー名を入れます。
時系列データの図化
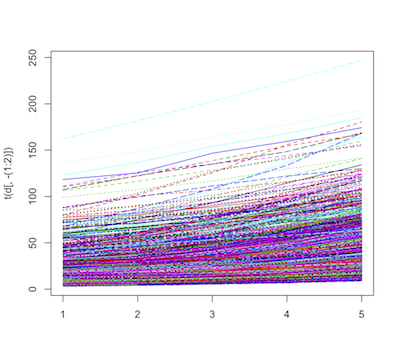
今回のデータは、時系列データです。それなら、時間に沿った変化を見たいところです。時系列な変化を作図するときは、matplot()を使います。
> matplot(t(d[, -(1:2)]), type="l")
なにやら色々呪文が並んでいますが......
matplot()は、各行が各自系列の時点 (今回で言うと年)になっていないといけません。しかし今回のデータは、列(横方向)に年が並んでいます。
t()は、転置行列(データフレームの行列を入れ替える)を行ってくれる関数です。
そこで、t(d[, -(1:2)])とすることで、元々のデータフレームの行列を入れ替えています(1〜2列目はプロット名と種名なので作図に入らないので除いておく)。 パッケージの読み込み
ここでパッケージという単語が出てきましたので、補足します。Rは様々な機能を持っていますが、その機能群の量が膨大すぎるので、最初は一部の機能しか読み込んでいません。
そのため、追加機能は「パッケージ」として配布されており、必要に応じてインストールする必要があります。パッケージをインストールするためには、
Windows:「パッケージ」→「パッケージのインストール」と進み、ダウンロードするミラーサーバを選ぶ(どこでもよい。日本だと筑波と兵庫がある)。その後、パッケージの一覧が表示されるので、必要なパッケージを選択してOKを押す(Ctrlキーで複数選択可能)。
Mac:「パッケージとデータ」→「パッケージインストーラ」とすすみ、パッケージ名を「パッケージ検索」の所に入力して検索。必要なパッケージが表示されたら「選択をインストール」からインストールする。
ただし、パッケージはインストールしただけでは機能しません 。Rに読み込んでやる必要があります。それが、先ほど見たlibrary(パッケージ名)という作業になります。
データの集計
さて、種やプロットごとにデータを取り出せるようになったことで、Aさんは「それぞれの種やプロットはどのような傾向を持っているのだろう?」ということに興味がわき始めました。ここでは、データを単独、あるいはカテゴリーごとに集計する方法を紹介します。
使う関数
mean():平均値を算出する。
sd():標準偏差を算出する。
min():最小値を算出する。
max():最大値を算出する。
table():カテゴリー数を算出する。
xtabs():カテゴリーごとに値を集計(2カテゴリー以上で力を発揮)。
tapply():カテゴリーごとに関数を適用。ゑくせるで言うところのピボットテーブルに当たる。 各種統計量の算出
基本的には、関数に統計量を算出したいデータを入れれば動作します。以下では平均値の齢を示しますが、標準偏差や最大値なども同様です。
> mean(d$DBH02)
カテゴリー数の算出
カテゴリーの列があると、それぞれのカテゴリーがいくつあるか知りたくなることがあります(各プロットに含まれる個体数とか)。カテゴリーごとのデータ数を知るためには、以下のようにします。
> table(d$Plot)
#2変数以上に拡張
> xtabs(~ Plot + Sp, d)
ちなみに、xtabs()は、~の前にデータを入れることで、カテゴリーごとの合計値を出すこともできます。例えば「プロット」かつ「種」ごとのDBH02の合計値を知りたいときは、
> xtabs(DBH02 ~ Plot + Sp, d)
とすれば計算できます。
カテゴリーごとに関数を適用
結構多用します。具体的には、「種ごとのDBHの平均値を知りたい」「プロットごとに最大個体サイズを出したい」などといった状況です。最初の例を実行する方法を以下に示します。
> tapply(d$DBH02, d$Sp, mean)
Sp01 Sp02 Sp03 Sp04 Sp05 Sp06 Sp07
13.511304 11.961657 14.638334 12.679400 10.904242 12.664050 12.940691
(以下省略)
tapply()は、(関数を適用するデータ, カテゴリー, 関数)という書き方になります。これは当然、2カテゴリー以上でも動作します。
> tapply(d$DBH02, d[, c("Plot", "Sp")], mean)
Sp
Plot Sp01 Sp02 Sp03
PlotA 9.636401 11.132252 16.309994
PlotB 8.404061 9.444711 16.000510
(以下略)
動作させる関数には、なにか計算する関数だけではなくて作図関数なども適用できます。
> par(mfrow=c(5, 5), mar=c(2, 2, 1, 1)) #作図関係のおまじない
> tapply(d$DBH02, d$Plot, hist, main="")
データの呼び方
ちょっと意識しにくいかも知れませんが、Rではデータ一つをとっても、形や並び方によって様々な呼び方をします。ここでは、データの呼び方をはっきりさせておきましょう。
1個のデータの種類
ちょっとイメージしにくいかも知れませんが、1個のデータを取ってみても種類がいくつかあります。具体的には以下のようです。
数字:numeric。1、3.5、-10など
文字列:character。"Tekito"、"Darui"など。
要因:factor。見た目は文字列っぽいのだが、水準(順位)が付いている。例えば本データ中のSp(d$Sp)は要因。
論理値:logical。TRUEまたはFALSE。
欠損:NA。これが入っていると動作しない関数があるので要注意(後述)。
非数:NaN。1/0とかやっちゃったりすると発生する。やっぱり関数の動作を妨げるので要注意。 塊としてのデータの種類
と、一つ一つのデータに種類があるわけですが、それらの集まりに関しても種類があります。具体的には以下のようです。
ベクトル:c()。構造などがない一つながりのデータ。あらゆる種類のデータを含めるが、同一ベクトル内で異なった形式の値を混在させることはできない 。むりくり異なった形式の値を混在させると、一番ランクの低い形式に合わされる。例えば、文字列が入っている場合は数字も文字列扱いになってしまう。 > test <- c(1, 2, "Tekito", TRUE)
> test
[1] "1" "2" "Tekito" "TRUE"
> test[1] + test[2]
Error in test[1] + test[2]
> 1 + 2
[1] 3
行列:matrix()。行列(縦と横)の形があるデータ。数字以外は含めない。
データフレーム:data.frame()。見た目は行列だが、数字以外も含める。実用的には最も多用する形式。行や列のラベルあるいは番号で行や列を取り出せる。行数の違う列が混在することはできない。
リスト:list()。構造や並び方が違うデータも無理矢理一つにできる。自分で作ることはあんまり無いが、統計や作図関数の結果を返したオブジェクトはリストになっていることが多い。
とりあえずこうしてみると、現在読み込んでいるdはデータフレームですが、PlotやSpなど一つ一つの列は「ベクトル」と見なすことができます。
データフレームの保存の仕方
上記のようにしていじったデータフレームは、ファイルとして保存できます。たとえばd2というオブジェクトにいじった結果がくっついているとしたら、
> write.csv(d2, file="new.csv", row.names=F)
> #new.csvというファイルとして保存。
とすれば保存できます。保存される場所は、現在の作業フォルダです。
欠損値NAへの対応
あれー?
> mean(d$DBH04)
[1] NA
2004年のDBHの計算をしようとして、Aさんはつまずいてしまいました。どうも、NAが入っていると関数がうまく動作しないようです。
このように、NAがあると色々と不都合が生じます。ここでは、NAの処理方法について解説します。
対処方法としては、主に以下の物があります。
関数の引数で対応。
NAを除去する。
NAを0に変換してしまう(欠損であることが0と等価である場合のみ有効) 関数の引数で対応
関数によっては、引数でNAを除いて実行することが可能です。
> mean(d$DBH04, na.rm=TRUE)
NAを除去する
ここでは、以下の関数を使います。
na.omit():NAを含む行を削除する。
is.na():NAならTRUE、そうでなければFALSEを返す
NAを含んだデータは必要ないと言うことであれば、NAを含む行を削除してしまうという手があります。
> nrow(d) #もともとのデータの行数
> d3 <- na.omit(d)
> nrow(d3)
[1] 4001 #NAを含む行が除かれ、行数が減少している
> summary(d3) #NAがDBHのどのデータにも含まれていない
ただしこの方法だと、全列を見て、NAがある箇所は全て除かれてしまうことになります。ある特定の列にだけ着目してNAを除去したいこともあると思います。ただし、NAかどうかを調べるだけでも特別な関数が必要になります。
> d[d$DBH04 != NA, ] #今までの知識ならこれで判定できそうだが......
Plot Sp DBH02 DBH04 DBH06 DBH08 DBH10
NA <NA> <NA> NA NA NA NA NA
NA.1 <NA> <NA> NA NA NA NA NA
NA.2 <NA> <NA> NA NA NA NA NA
(以下略)
といったように、NAかどうかを判定するためには、それ専用の関数が必要になります。
> is.na(d$DBH04)
こうすると、とりあえずNAかどうかは判定できているようです。で、今はNAでない 部分が欲しいので、否定である!をつけて、以下のようにします。
> d[!is.na(d$DBH04), ]
NAを0に変換する
手順としては、NAかどうかを調べ、NAなら0、そうでないなら元データを返すという作業をします。
このような条件分岐(TRUEの場合、FALSEの場合)はifelse()という関数で行います。具体的な手順としては、以下のようにします。
> d$DBH04a <- ifelse(is.na(d$DBH04), 0, d$DBH04)
上記からわかるように、ifelse()はifelse(条件式, TRUEの場合, FALSEの場合)という書き方になります。
NAから生残データを生成
ここはおまけです。
今はデータとしてサイズ(DBH)だけが入力されています。そして死亡した場合は欠損(NA)が入力されています。
ですが、このままですと生残を作図したり解析したりするのには不便です。生残は生残1、死亡0としておくと便利です。
そこで、サイズデータとNAを逆手にとって、生残データを作ってみましょう。具体的には、NAの場合は死亡なので0、それ以外の場合は生残なので1にすればいいわけです。
> d$S04 <- ifelse(is.na(d$DBH04), 0, 1)
これができるようになると、わざわざデータシートに生残と成長のデータ両方を打ち込む必要がなくなります。
データ同士の結合
Aさんは過去からの測定データを受け継いだわけですが、自らの研究でただ続きの成長・生残データを取るだけではつまらないと思いました。そこで、調査地ごとの光環境と水分条件を測定しました(環境データは
こちら )。
> e <- read.csv("env.csv")
> head(e)
Plot Light Water
1 PlotA 0.4847369 19.98155
2 PlotB 0.5566825 21.83956
(以下略)
さて、環境データを取ったのはいいのですが、このデータは「Plotごと」のデータです。これを個体のデータにくっつけようとすると、10000個のデータについて一つ一つ環境データをくっつけると!?とてもじゃないですが、やってられません。
しかし、個体のデータと環境データは「プロット」という共通の記号をもっています。これを目印にしてデータを結合できないでしょうか?
こういったデータ同士の結合には、merge()が便利です。
> d2 <- merge(d, e)
> head(d2, 2)
Plot Sp DBH02 DBH04 DBH06 DBH08
1 PlotA Sp56 14.773116 16.737987 19.31643 24.61452
2 PlotA Sp46 10.959117 13.831113 17.40913 23.60213
DBH10 S10 Light Water
1 NA 0 0.4847369 19.98155
2 30.27258 1 0.4847369 19.98155
merge()は、2つのデータフレームに共通な「列名」を目印にしてデータを結合させるという機能があります。
データ解析
さて、上記のようにして、徐々にデータの思い通りの部分がみれるようになってきたAさん。そこでそろそろ本題である、「生残にどのような要因が影響しているのか?」について検討したいところです。
まずは、上記の疑問について図で見てみることにしましょう。今回のデータで要因として考えられるのは、Spや先ほどの環境データ(Light、Water)ですね。
データの図化
まずは、必要なデータを読み込みます。
> d <- read.csv("base.csv")
#生残データを作る
> d$S10 <- ifelse(is.na(d$DBH10), 0, 1)
#環境データを読み込んで結合
> e <- read.csv("env.csv")
> d2 <- merge(d, e)
生残
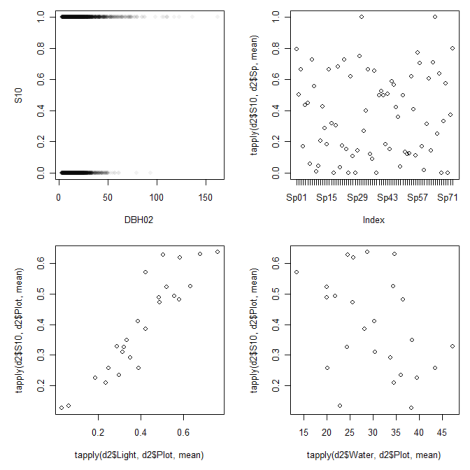
では、実際に生残と考えている要因の関係がどうなっているか、見てみましょう。
種によって生残率が異なり、明るく乾燥しているほど生残率は高いように見受けられます。しかし、複数の要因が同時に作用しているため、これらの作図だけではどの要因が成長や生残に影響しているのか判然としません。
現象をモデル化する
こうした状況で、興味のある現象と考えられる要因の関係を検討するためには、現象のモデル化が必要になります。
えっ、別に俺モデル屋じゃないし......と思う人が多いかと思います。しかし、統計解析する時点で、それはモデルを組むという作業をしている のです。検定も、立派な統計モデルです。
すなわち、データを解析しようとするときには、データに対して何らかのモデルを考える必要があります 。
統計モデルの部品~決定論的モデルと確率論的モデル
統計モデルは、決定論的モデル と確率論的モデル に分けられます。
決定論的モデル:説明変数と応答変数の関係性を示したもの。自分がどう現象を捉えているかといってもいい。
確率論的モデル:得られる現象がどのような確率的変動をもって生じるかに関する仮説。
統計的モデリングを行ううえで、これらの存在を意識することが重要です。決定論的モデルはそれぞれの減少に対して研究者が考えることですので、ここでは確率論的モデルについて紹介したいと思います。
確率論的モデル
得られるデータが完全に決定論的モデルに従って得られることはまずありません。というのは、
などにより、決定論的モデルでは説明しきれないデータしか得られないからです。ここで大事なのは、決定論的モデルで説明しきれない誤差がどのような形の誤差になっているか ということです。
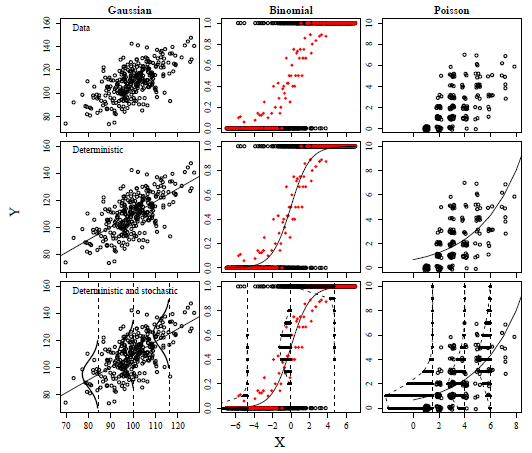
これを、以下の図で説明したいと思います。
この図は、
1行目:データ
2行目:データと、決定論的モデルでの予測値(線)
3行目:決定論的モデルと想定している誤差の分布
を示しています。
決定論的モデルに含まれる要因の係数(切片や傾き)は、データを最もよく説明できるように決定されます。では、「データを最もよく説明できる」基準とはなんでしょうか?
それが、「決定論的モデルで説明できない誤差を最も小さくする」ことです。しかし、上の図を見ていただいても分かるように、データの種類によって誤差の分布は変わってきます。
そのため、「誤差を最も小さくする」ためには、「データがどのような誤差を持ちうるか」、すなわち、確率論的モデルを決定する必要があるのです。
かつての統計モデルは正規分布を仮定するものがほとんどだったため、確率論的モデルとして正規分布を仮定する、それができない場合はデータを正規分布するように変数変換するといったことが行われてきました。しかし、生残率などは0~1の間にしかなりませんし、0、1、2個といったカウントデータは0より小さくならない上、誤差が等分散ではありません。これらには、異なる確率分布を考える必要があります。
こうした、様々な確率分布のデータに対し、自分が考える仮説の影響を検討する方法は様々物がありますが、比較的汎用性の高い統計モデルとして、一般化線型モデル(Generalized Linear Model:GLM)があります。以下ではGLMについて解説します。
GLM&モデル選択
自力で尤度を計算
実際に自分の手で尤度を求めて見ましょう。なお、今回は単純化のため、光が生残に影響しているか?というモデルについて検討します。
こちらのファイル を開いてください。
このゑくせるファイルはbase.csvから2010年の生死、光環境、各データについて尤度、対数尤度、そしてモデル全体の尤度と対数尤度が示されています。
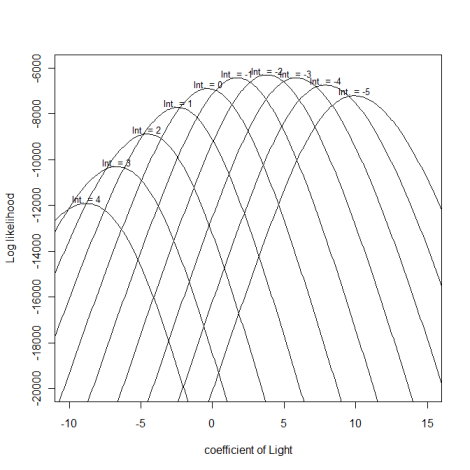
そして、推定したいパラメータである切片と光の傾き(係数) の値を変えると、モデル全体の尤度および対数尤度の値が変化します。(対数)尤度が最大となるときの切片および傾きが、最尤推定値ということです。
切片や傾きを変化させたときの対数尤度の挙動
で、探索的に最尤推定値を求めるのは大変なので、原理がわかった後はRのglm()関数に任せましょう。
GLMで指定しなければならないこと
GLMを行うためには、一般的に以下のように入力します。
> result <- glm(y ~ x1 + ...,
+ family = 誤差構造(リンク関数), データ名)
見てもわかるとおり、モデル式、誤差構造、リンク関数なるものを指定する必要があるわけです。モデル式は作図の結果から各自検討することですので、残りの2つについて解説します。
誤差構造とは、応答(従属)変数の分布の形を示します。つまり、データがどのような確率分布をしているかを指定するわけです。
gaussian: いわゆる正規分布。
binomial: 二項分布。生死データなどで使う。
poisson: ポアソン分布。カウントデータ(1個、2個...)で使う。
リンク関数とは、データから得られた期待値を変換し(注!観測値そのものを変換しているわけではない)、線形予測子を構築するためのものです。各誤差構造に対し、通常用いられるリンク関数は以下のようです。
gaussianの場合: identify(特に変換しない)
binomialの場合: logit(ロジット変換)
poissonの場合: log(対数変換) GLMの結果の見方
GLMの結果を見るためには以下のようにします。
> res <- glm(S10 ~ Sp + DBH02 + Light + Water, family=binomial, d2)
> summary(res)
Call:
glm(formula = S10 ~ Sp + DBH02 + Light + Water, family = binomial,
data = d2)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.0201 -0.6014 -0.1823 0.6581 2.9649
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.102e+00 2.461e-01 -4.478 7.54e-06 ***
SpSp02 -1.633e+00 2.590e-01 -6.305 2.88e-10 ***
SpSp03 -9.401e-01 6.070e-01 -1.549 0.121417
(一部省略)
SpSp72 -2.527e+00 2.638e-01 -9.580 < 2e-16 ***
SpSp73 -3.537e-01 8.659e-01 -0.408 0.682920
DBH02 7.888e-02 3.392e-03 23.255 < 2e-16 ***
Light 5.854e+00 1.938e-01 30.211 < 2e-16 ***
Water -1.843e-02 3.553e-03 -5.186 2.15e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 13461 on 9999 degrees of freedom
Residual deviance: 8185 on 9924 degrees of freedom
AIC: 8337
最低限見るべきものとしては、
Coefficients: Estimateが推定された係数
deviance: Null devianceが切片項のみのdeviance、Residual devianceが説明変数を投入したときのdeviance
が挙げられます。devianceとはあてはまりの悪さを示し、これが小さいほどデータによくあてはまっていることを示しています。
変数の選択方法(モデル選択。どの変数の影響が強いか?)としては、以下で述べるAICが一般的に用いられます。
影響が強い変数の選択(モデル選択)
AICは、
AIC = −2 × maximum log likelihood + 2p
と定義され、あてはまりとパラメータ数のバランスをとったものであり、AICが小さいほどよいモデルとされます。AICによるモデル選択を行うためには、stepAIC()を使います。
> library(MASS)
> stepAIC(res)
#最終的に決定されたモデルが表示される。
ここで決定されたモデルに含まれる変数は意味のある変数であり、含まれなかった変数はそうではない変数、と考えるわけです。
ちなみに、AICは上記のようにあてはまりとパラメータ数のバランスから「相対的に良いモデル」を選んでいるのであって、「ベストなモデル」を選択しているわけではありません。
GLMの推定結果の取り出し方
GLMの推定結果は、主な部分はsummary()で取り出せることはわかりました。しかし、この推定結果を使って図を書いたり結果を検証することはよくあります。
そんなときに、summary()の結果を目で見て数字をいちいち書き出していたのではきりがありません。ここでは、GLMの推定結果の取り出し方を解説します。
GLMの結果は、あるオブジェクトに格納していると思います。これにnames()関数を適用すると、どのような名前で結果が保存されているかわかります。
> res <- glm(S10 ~ Sp + DBH02 + Light + Water, family=binomial, d2)
> names(res)
[1] "coefficients" "residuals" "fitted.values"
[4] "effects" "R" "rank"
[7] "qr" "family" "linear.predictors"
[10] "deviance" "aic" "null.deviance"
[13] "iter" "weights" "prior.weights"
[16] "df.residual" "df.null" "y"
[19] "converged" "boundary" "model"
[22] "call" "formula" "terms"
[25] "data" "offset" "control"
[28] "method" "contrasts" "xlevels"
すると、思ったよりいろいろな結果が入っていることがわかります。例えば推定された係数(切片や傾き)などを取り出したい場合は、
> res$coefficients
(Intercept) SpSp02 SpSp03 SpSp04 SpSp05 SpSp06
-1.10218796 -1.63314890 -0.94008372 -3.88273766 -2.16474249 -2.16506611
(一部省略)
SpSp73 DBH02 Light Water
-0.35369602 0.07887668 5.85433745 -0.01842619
といったように、係数を得ることができます。
実は、先ほど使ったsummary()の結果にもいくつかの結果が含まれています。
> res2 <- summary(res)
> names(res2)
[1] "call" "terms" "family" "deviance"
[5] "aic" "contrasts" "df.residual" "null.deviance"
[9] "df.null" "iter" "deviance.resid" "coefficients"
[13] "aliased" "dispersion" "df" "cov.unscaled"
[17] "cov.scaled"
#例えば
> coefficients(res2)
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.10218796 2.461428e-01 -4.47784032 7.540196e-06
SpSp02 -1.63314890 2.590099e-01 -6.30535335 2.875371e-10
SpSp03 -0.94008372 6.069544e-01 -1.54885402 1.214168e-01
(一部省略)
SpSp72 -2.52684304 2.637553e-01 -9.58025389 9.680667e-22
SpSp73 -0.35369602 8.658808e-01 -0.40848117 6.829205e-01
DBH02 0.07887668 3.391775e-03 23.25528176 1.257841e-119
Light 5.85433745 1.937843e-01 30.21058124 1.720015e-200
Water -0.01842619 3.552978e-03 -5.18612458 2.147152e-07
カテゴリ変数の推定結果の見方
さて、先ほどの推定された係数を見た方は気づいたかと思いますが、種の係数については種1(Sp1)の値がありません。
これは計算が失敗したとかいうことではなく、Rでのカテゴリ変数の処理の仕方なのです。具体的にはアルファベット順で最初のカテゴリとなるカテゴリの値が切片に含まれていて、それに対する相対的なほかのカテゴリの係数が示されている のです。
すなわち、
#Spの係数
-1.10218796
#Sp2の係数
(-1.10218796) + (-1.63314890)
#Sp3の係数
(-1.10218796) + (-0.94008372)
ということです。
ちなみに、切片となるカテゴリ(レファレンスカテゴリ)を変更する方法は2つあります。
relevel()を使う:レファレンスカテゴリだけを指定
factor()を使う:レファレンスカテゴリを含め、カテゴリのすべての順番を指定
それぞれの使い方を、以下に示します。
d2$SP2 <- relevel(d2$Sp, ref="Sp2") #Sp2をレファレンスカテゴリにする
d2$SP3 <- factor(d2$Sp, levels=c("Sp2", "Sp72", ....(面倒なんで省略), "Sp1")
こうやるとどうなっているか、ご自身でSpの代わりにSP2やSP3を使って解析して確認してみましょう。
推定結果の予測値の取り出し
推定結果が取り出せるようになったので、推定結果とデータの関係を見て、きちんと推定できているか確認しましょう。
切片や係数の推定結果が得られたので、各データについて「生残確率(予測値)」を計算することができます。
GLMによる予測値の計算で厄介なのが、GLMではリンク関数を使っているので、予測値を出すためにはリンク関数を解除する必要があることです。下記のリンク関数について、リンク関数を解除するための方法(逆リンク関数)は以下のようです。
identify: 特に変換する必要なし
logit: 1/(1+exp(-x))。xに予測値を入れる
log: exp(x)。xに予測値を入れる
今回はlogitですので、それを元に戻して予測値を計算してみましょう。
まず、推定された係数を取り出します。
> co <- coefficients(res)
> co[1]
(Intercept)
-1.102188
これで、coというオブジェクトに推定された係数をくっつけることができました。coに入っている順番は、
> names(co)
で見ることができます。
今回のモデルは、
生残 = 樹種+2002年のDBH+光+水
というものでした。なので、各データについて、2002年のDBHと光と水と樹種の推定結果を使った予測値を入れればいいことになります。では、計算してみましょう。
> d2$EstGLM <- 1/(1+exp(-(co[1] + co[as.numeric(d2$Sp)+1]
+ co[74]*d2$DBH02 + co[75]*d2$Light + co[76]*d2$Water)))
1/(1+exp(-())というのは上で解説したように、logitの逆リンク関数(logistic変換)です。co[]というのは、上で取り出した係数で、1でしたら1番目に入っている切片、2でしたら2番目に入っているSp2の推定された係数、...ということになります。
ちょっと複雑なのが、種の係数ですね。各データ(行)についてどの種か判定して、その種の係数を取り出す必要があります。
その他こまごま
とりあえず書き散らしたものがここ にあります。
IOVを算出するスクリプトは、ここ にあります(注!現在ではうまく動作するかわかりません)。 おわりに
Aさんの解析までの道のりは、とりあえず一段落しました。しかし、データの見方にしても解析の仕方についても、まだまだ不十分です。不十分を詰めていくための方法の助けになる内容を、以下のページに掲載していますので、必要に応じてご覧ください。
最終更新:2015年12月27日 20:19