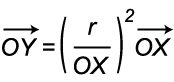What's quasi-sphere?
A quasi-sphere is a kind of fractal shapes in the three dimensional space (). This shape is derived from a quasifuchsian group in a pure mathematical way. In this site, we have many pictures of quasi-sphere, which are derived from sphairahedra and inversions. Dr. Y. Araki and I construct many examples of sphairahedra in our paper. These fractal figures are the first images in the world.
What's inversion?
There are two kinds of inversions. One is an inversion of a circle and the other is an inversion of a sphere. In any case, inversion map is defined by the same formula. Let C(O,r) be a circle (or a sphere) with a center O and a radius r . Let f be an inversion of C . For a point X in a plane ( or in a space) , its inversion image Y=f(X) is defined as follows.
Here are some elementary propositions about inversion.
- If X is on C , then Y also lies on C .
- If X is inside of C , then Y is outside of C .
- If X coincides to the center O of C , then Y is the infinity point .
- Let D be another circle (or sphere) then the image f(D) is also a circle (or sphere.) If D be a circle with O then f(D) is a straight line (or a plane.)
- If C is a straight line (of a plane), that is, O is the infinity point and r is infinity, then inversion is a mirror reflection of C .
What's sphairahedron?
A sphairahedron is a new word made from two words, ‘sphaira-‘ (=spherical) and ‘-hedron' (=polyhedron). Usually we consider a polyhedron as an area surrounded by planes. A sphairahedron is an area surrounded by spheres or planes. (We may regard a plane as a kind of spheres, because a plane is a sphere thru the infinity point.)
A sphairahedron has faces, edges and vertices as a polyhedron does. That is, each sphere is called a face. Each intersections of two faces is called an edge. Each intersection of three (or more) edges is called a vertex.
A sphairahedron is called regular if the dihedral angel of each edge divides 180 degree. (For example, 90 degree, 60 degree, 45 degree, and 30 degree.)
sphairahedron is called ideal if for each vertex, three (or more) edges are mutually tangent at the vertex.
The following figure is an example of a regular (all dihedral angles are 60 degree) ideal sphairahedron.
How many sphairahedra in the world?
There are many, indeed. :-) I have researched all of ideal regular sphairahedra with at most 6 faces in our paper [1], but up to now there are lots of ideal regular sphairahedra are known. [1] says that there are 8 polyhedral-types of ideal regular sphairahedra and for each type, there are many combinations of dihedral angles. In the gallery page, there are many pictures, but they are derived from sphairahedra of cubic type. There are 7 combinations of dihedral angles for cubic-type ideal regular sphairahedron and I call them type A, … , type G.
Can I draw these figures by myself?
Ah….. Yes and No. ;-) That is, now (March, 2003), there are no plan to open the source to draw these quasi-spheres. If you understand all of concepts to draw quasi-spheres, then it is not hard to make by yourself. I'm using Perl to make data of quasisphere and using PovRay to make rendered images.
What's definition of quasi-sphere?
Let's fix an ideal regular sphairahedron P. Next consider a tiling defined by the sphairahedron and inversion transformations. That is, all faces of P are spheres (or planes), so we can map P by the inversions of faces. If P has 6 faces, then there are 6 images of P by these inversions and they are neighbor of P. Any image of a sphairahedron by an inversion is also a sphairahedron. So we can iterate mapping by inversions of the faces. And we can get a tiling of sphairahedra. Here remark that the condition ‘regular' is needed. Because we choose one edge of P and iterate inversions such that the image contains the edge, and if the dihedral angle divides 180 degree, then within finite times, one of iterated inversion images coincides P itself, but if it isn't, we cannot make a tiling.
OK. To understand this tiling well, imagine an easy case. Consider P as a cube. All dihedral angles are 90 degree, so it is regular sphairahedron. Faces are planes, so the inversion of a face is a reflection map of a face. We can make a tiling of cubes by reflections of faces very easily. And the total space of this tiling is the whole space.
Again, let P be an ideal regular sphairahedron. And let's make a tiling of sphairahedron using inversions of the faces of P. You must be surprised if you hear that in this case, the total space of the tiling (we call it T) is not the whole space. If P doesn't contain the infinity point, then the total space T of the tiling is a finite shape like a ball. It is known that in almost cases, the surface (boundary) of T is fractal shape. This is a quasi-sphere.
What's quasifuchsian group?
If you can construct a quasi-sphere from a tiling of sphairahedra, it appears a quasifuchsian group here. Do you know ‘group' in mathematics? If you do, I'll teach you later.
Reference
[1] Ahara K. and Araki Y., “Sphairahedral Approach to Parameterize Visible Three Dimensional Quasi-Fuchsian Fractals”, CGI2003
[2] Ahara K. and Araki Y. , “Ideal sphairahedra and quasifuchsian groups”, preprint, 2002
最終更新:2011年09月22日 12:14