離散的な曲率・捩率の計算 - musaka @ ウィキ

---

	e11[c_][t_] := D[c[u], u]/Sqrt[D[c[u], u].D[c[u], u]] /. u -> t;
	e22[c_][t_] := Cross[e33[c][t], e11[c][t]];
	e33[c_][t_] := Cross[
		D[c[u], u], D[c[u], {u, 2}]]/
			Sqrt[Cross[D[c[u],u],D[c[u],{u,2}]].Cross[D[c[u],u],D[c[u],
		{u, 2}]]] /. u -> t;

---

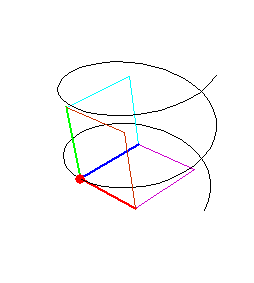
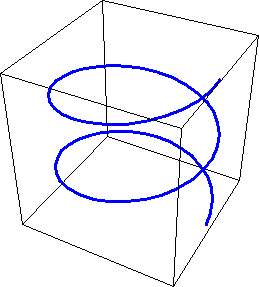
hel[t_] = {Cos[t], Sin[t], t/6};

---

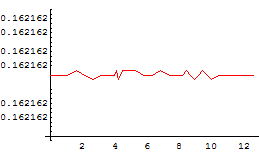
ここでは隣接する従法線ベクトルのなす角を離散的な捩率とする。
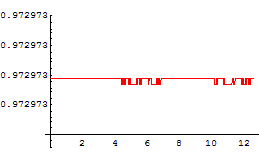
隣接する接線ベクトルのなす角を離散的な曲率とする。
離散的な曲率は常に正をとり、
離散的な捩率は一つ前の従法線ベクトルに対して,ひとつ前の接戦ベクトルを軸にして
時計回り(外側)に回転するとき正
反時計回り(内側)に回転するとき負をとるようにする。

for(int i=0;i<(int)cc.vectors.size()-1;i++)
{
	cc.Curvatures.push_back(
		acos(
			GetCosFromVector(
				cc.vectors.at(i).x,cc.vectors.at(i).y,cc.vectors.at(i).z,
				cc.vectors.at(i+1).x,cc.vectors.at(i+1).y,cc.vectors.at(i+1).z
			)
		)
	);

}	
for(int i=0;i<(int)cc.normals.size()-1;i++)
{
	double theta=acos(	
			GetCosFromVector(
				cc.binormals.at(i).x,cc.binormals.at(i).y,cc.binormals.at(i).z,
				cc.binormals.at(i+1).x,cc.binormals.at(i+1).y,cc.binormals.at(i+1).z
			)
		);
	if(0 < 	GetCosFromVector(
			cc.normals.at(i).x,cc.normals.at(i).y,cc.normals.at(i).z,
			cc.binormals.at(i+1).x,cc.binormals.at(i+1).y,cc.binormals.at(i+1).z
		)
	)
	theta*=-1;//従法線ベクトルが　法線ベクトルの方向に回転するとき　捩率が負　をとるようにする			
	cc.Torsions.push_back(theta);
}
curves.push_back(cc);

---

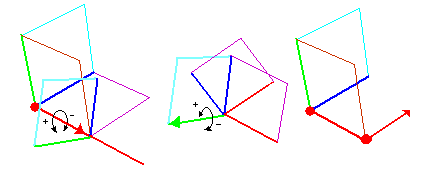
1.最初の動標構A　接線ベクトルe11,　従法線ベクトルe22,　主法線ベクトルe33がある。
2.動標構Aをコピーして動標構Bをつくる。e11'e22'e33'
3.動標構Bをe11を軸にして離散的な捩率分だけ回転させる。
　反時計回りの回転が負　時計回りが正
4.そのあとさらに、動標構Bをe22'を軸にして離散的な曲率分だけ回転させる。
　反時計回りが正

これを繰り返して,線分で構成される曲線を,離散的な曲率・捩率から逐次復元していく。

---

	RotateVectorByUnitVector(
		curves.curves.at(curve_at).Torsions.at(1),
		curves.curves.at(curve_at).binormals.at(1).x,
		curves.curves.at(curve_at).binormals.at(1).y,
		curves.curves.at(curve_at).binormals.at(1).z,
		curves.curves.at(curve_at).vectors.at(2).x,
		curves.curves.at(curve_at).vectors.at(2).y,
		curves.curves.at(curve_at).vectors.at(2).z,
		&tmpx,&tmpy,&tmpz
		);
		tmptheta=GetCosFromVector(
				curves.curves.at(curve_at).binormals.at(1).x,
				curves.curves.at(curve_at).binormals.at(1).y,
				curves.curves.at(curve_at).binormals.at(1).z,
				tmpx,tmpy,tmpz);
		
		RotateVectorByUnitVector(
			curves.curves.at(curve_at).Curvatures.at(2),
			curves.curves.at(curve_at).vectors.at(2).x,
			curves.curves.at(curve_at).vectors.at(2).y,
			curves.curves.at(curve_at).vectors.at(2).z,
			tmpx,tmpy,tmpz,
			&tmpx2,&tmpy2,&tmpz2
		);
		tmptheta=GetCosFromVector(
			curves.curves.at(curve_at).vectors.at(2).x,
			curves.curves.at(curve_at).vectors.at(2).y,
			curves.curves.at(curve_at).vectors.at(2).z,
			tmpx2,tmpy2,tmpz2);
		glPushMatrix();
		glColor3f(0,0,1);
			bvh.RenderBone(
				(float)curves.curves.at(curve_at).points.at(3).x,
				(float)curves.curves.at(curve_at).points.at(3).y,
				(float)curves.curves.at(curve_at).points.at(3).z,
				(float)(curves.curves.at(curve_at).points.at(3).x+tmpx2*7.53),
				(float)(curves.curves.at(curve_at).points.at(3).y+tmpy2*7.53),
				(float)(curves.curves.at(curve_at).points.at(3).z+tmpz2*7.53),
				0.2f);
		glPopMatrix();