数式だけで具体的状況を表現し切ることは無理(か?)
このページの内容は、開米瑞浩@kmic67による個人的な論考です。ご意見、提案などはtwitter #掛算 タグつきで @kmic67 へリプライをください。
このページのPDF版は→数式だけで具体的状況を表現し切ることは無理(PDF)
数式だけで具体的状況を表現し切ることは無理
まずはこういうシーンを考えてみてください。

ここで、太郎君は問題を解くためにいくつかの「知的作業」を行っています。その「知的作業」を、「目的」と「手段(道具)」に分解すると、次のようになります。
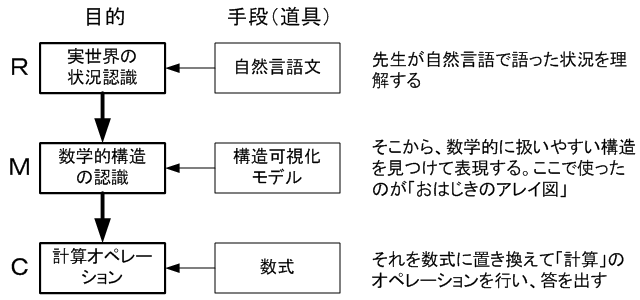
上記3つの「目的」欄はそれぞれ別なワークであることに注意してください。単純な文章題であっても、それを解くためにはこの3つのワークを連携して行わなければなりません。
ところで、問題は、多くの算数の練習問題が 「自然言語文」 を示したあとは 「数式」→「答」 というフォーマットで構成されているということです。
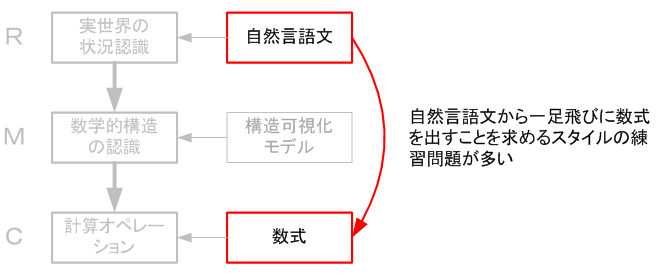
もし、子供の 「R:実世界の状況認識」 と 「M:数学的構造の認識」 の力が十分ついていれば、自然言語文から数式へ一足飛びに向かわせても問題は起きません。
しかしそれが不十分だと、困ったことになります。実際、「計算問題はできても、文章題ができない」というのは算数ができない子の典型的な悩みです。
これは、
計算オペレーションはできていても、「R:実世界の状況認識」 と
「M:数学的構造の認識」 ができていない子が大勢いる
ことを示しています。
では、ある子供がたとえば「かけ算」を勉強し始めたとき、先生はその子が R と M のワークでつまずいていることをどうやって察知するのでしょうか?
・・・・という悩みを抱えた先生が、あるときうまい手を思いついたのでしょう。
立式の順序を「1つ分の個数 × いくつ分」に固定させれば、
基本的な「R:実世界の状況認識」が出来ていない子を発見しやすい!
というものです。この方法には、非常に限定的ではあっても一定の効果はありそうです。確かに、ごくごく基本的な「R:実世界の状況認識」も出来ていなければ、このルールには対応できません。
しかし、いいことばかりではありません。というよりこの方法には欠点のほうがはるかに多いと思われます。
欠点1:すぐに抜け道ができる
欠点2:真の算数の力がつかない
そもそも数式はCのための道具なのであって、それを使ってRやMの力を測ろう、というのは根本的に無理な話です。RとMについてはそれ自体のトレーニング方法を考えるべきで、「数式」を使うのは本末転倒以外の何者でもありません。そんな無理でお茶を濁していたのでは、結局、RとMの力がつかないままで終わってしまいます。
欠点3:社会的かつ数学的に間違い
「かけ算の立式順序のルール」は、実際には社会的にも数学的にも存在しません。存在しないルールを小学校で徹底して教える、というのはおかしな話です。
欠点4:子供のやる気と先生への信頼を破壊する
「かけ算の立式順序のルール」を徹底しようとすると、数学的に正しい解答をローカルルールで不正解にする、というケースが多発します。これを子供に納得させるのは難しく、本来正しい解答を不正解にされた子供のやる気を損ない、先生への不信感をつのらせる結果を産みます。
では、どうすれば良いのか?
単純な話で、RとMについては、Cと混ぜずにそれだけを目的としたトレーニングのカリキュラムを作るべき、というのが本筋です。(「かけわり図」は特にMのための有力な一手段)
最終更新:2014年07月23日 00:32


