Limb darkening_wiki 翻訳ノート - 夢を語る

　１．基礎理論のための参考資料：Limb Darkening - Wiki　の翻訳ノート
英語の翻訳はあまり自信がないが、専門用語の関係を明確にしておくための単なるノートである。

Limb darkening
Limb darkening is an optical effect seen in stars (including the Sun), where the center part of the disk appears brighter than the edge or limb of the image. Its understanding offered early solar astronomers an opportunity to construct models with such gradients. This encouraged the development of the theory of radiative transfer.

外縁暗光（一般的には周辺減光と訳されているが、こちらの方が意味がわかり易いと思う。）
外縁暗光は恒星（太陽も含む）の中に見られる光学的効果のことであり、円盤の中央部分は端部分すなわち外縁部分より明るく見える現象を指す。初期の太陽天文学者たちはその様な外縁暗光を引き起こす理論の構築を試みた。このことが、放射伝達理論の発展を促した。

Crucial to understanding limb darkening is the idea of optical depth. A distance equal to one optical depth is the thickness of the absorbing gas from which a fraction of 1/e photons can escape. This is what defines the visible edge of a star since it is at a few optical depths that the star becomes opaque. The radiation reaching us is closely approximated by the sum of all the emission along the entire line of sight, up to that point where the optical depth is unity. When we look near the edge of a star, we cannot "see" to the same depth as when we look at the center because the line of sight must travel at an oblique angle through the stellar gas when looking near the limb. In other words, the solar radius at which we see the optical depth as being unity increases as we move our line of sight towards the limb.

外縁暗光を理解するための重要な鍵はoptical depth（光学的深さ）である。1 optical depthに等しい距離は、1/eの割合の光子が逃げていくことができる吸収ガスの層の厚さである。これが、星の見えている端を決めている何かであり、数optical depthのところでその星は不透明になる。我々に届くその星の放射光は、すべての視線に沿ってのすべての発光を、optical depthが１のところまで合計することにより、厳密に見積もることができる。我々が星の端近くを見たとき、我々が星の中央を見たときと同じ深さまで見ることができない。なぜなら、外縁付近を見たとき、視線は星のガスを斜めの角度で通過しなければならないからである。言いかえると、我々がかろうじて見ることができる単位１のoptical depthに相当する場所の星の中心からの距離(solar radius)は、我々の視線が外縁部に行けば行くほど増大する。

The second effect is the fact that the effective temperature of the stellar atmosphere is (usually) decreasing for an increasing distance from the center of the star. The radiation emitted from a gas is a strong function of temperature. For a black body, for example, the spectrally integrated intensity is proportional to the fourth power of the temperature (Stefan-Boltzmann law). Since when we look at a star, at first approximation the radiation comes from the point at which the optical depth is unity, and that point is deeper in when looking at the center, the temperature will be higher, and the intensity will be greater, than when we look at the limb.

2番目の効果は、恒星の大気の有効温度は（一般的に）星の中心からの距離が増大すればするほど減少するという事実である。ガスからの放射光は温度に強く依存している関数で表される。例えば黒体放射の場合、スペクトルに対して積算した強度は温度の4乗に比例している(Stefan-Boltzmann law)。我々が星を見たとき、最初の近似で、放射光はoptical depthが１のところから到来し、その場所は星の中心を見たときほど深くなる。そのため、我々の視線が星の中心に近づけば近づくほど見えている場所の温度は高くなり、放射光強度は増大する。

In fact, the temperature in the atmosphere of a star does not always decrease with increasing height, and for certain spectral lines, the optical depth is unity in a region of increasing temperature. In this case we see the phenomenon of "limb brightening"; for the Sun the existence of a temperature minimum region means that limb brightening should start to dominate at far-infrared or radio wavelengths. Outside the lower atmosphere, and well above the temperature-minimum region, we find the million-degree solar corona. For most wavelengths this region is optically thin, ie has small optical depth, and must therefore be limb-brightened if spherically symmetric.

実際には、恒星の大気の温度は高度が高いほどいつも減少するわけではなく、ある特定のスペクトル線において、温度増大領域の中でoptical depthが１となっている。この場合、我々は"limb brightening"（外縁明光：一般的には周辺増光と訳されるが、外縁暗光の反対語としてこのように訳した。）という現象を見ることができる。太陽において温度極小領域の存在は、外縁明光が遠赤外や電波波長で顕著に表れ始めなければならないことを意味する。低位大気の外側、そして、温度極小領域の十分上で、我々は百万度の太陽コロナを見出す。ほとんどの波長領域でこの領域は光学的に薄く、すなわち、小さなoptical depthを持っている。それゆえ、もしそれが球対称であるならば外縁明光が起こらなければならない。

Further complication comes from the existence of rough (three-dimensional) structure. The classical analysis of stellar limb darkening, as described below, assumes the existence of a smooth hydrostatic equilibrium, and at some level of precision this assumption must fail (most obviously in sunspots and faculae, but generally everywhere). Instead, the boundary between the chromosphere and the corona consists of a very complicated transition region best observed at ultraviolet wavelengths only observable from space.

さらなる問題として、（3次元的に）でこぼこした構造の存在がある。以下に記述したように、星の外縁暗光の古典的解析は滑らかな流体静力学的平衡の存在を仮定しているため、ある程度正確にしようとするとこの仮定は失敗するに違いない（もっとも明らかに黒点や白斑において失敗するが、一般的にはどこにおいても失敗する）。そのかわり、クロモスフィア（彩層：コロナの下の層のこと）とコロナの間の境界領域は大変複雑な遷移領域からなり、宇宙空間からのみ観測可能である紫外波長ではっきりと観測されている。

Calculation of limb darkening

Limb darkening geometry. The star is centered at O  and has radius R . The observer is at point P  a distancer  from the center of the star, and is looking at point S  on the surface of the star. From the point of view of the observer, S  is at an angle θ from a line through the center of the star, and the edge or limb of the star is at angle Ω.

In the figure on the right, as long as the observer at point P is outside the stellar atmosphere, the intensity seen in the direction θ will be a function only of the angle of incidence ψ. This is most conveniently approximated as a polynomial in cos(ψ)

右図において、P点の観測者が星の大気の外にいる限り、θ角方向から見える放射光強度は入射角ψだけの関数であろう。この関数はcos(ψ)の多項式で近似すると便利である。

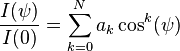
where I(ψ) is the intensity seen at P along a line of sight forming angle ψ with respect to the stellar radius, and I(0) is the central intensity. In order that the ratio be unity for ψ=0, we must have:

ここで、I(ψ)は角度ψの視線に沿ってP点で観測される星の半径に関連する放射光強度であり、I(0)は中央の放射光強度である。ψ=0のときこの比は１になるので、次式が成立する。

For example, for a Lambertian radiator (no limb darkening) we will have all a_k=0 except a₀=1. As another example, for the sun at 550 nm, the limb darkening is well expressed by N=2 and

例として、ランバーチャン放射体(Lambertian radiator:Lambertのコサインの法則が成立する放射体のことをランバーチャン(Lambertian)と言う。滑らかな黒体に近い物体の場合にほぼ成立）のとき、 a₀=1を除く全てのa_k=0となる。別の例として、太陽の550nmにおいては、N=2 であり、

(See Cox, 2000). Note - the equation for limb darkening is sometimes more conveniently written as:

ノート：外縁暗光の式はしばしば次式のように記述するとより便利である。

which now has N  independent coefficients rather than N+1  coefficients which must sum to unity.

We can convert from ψ to θ using the relationship:

これは、合計して１となるN+1個の係数を持つよりも、それぞれ独立したN個の係数を持つようになる。
次の関係式を使うと ψ から θへ変換できる。

where Ω is the angle from the observer to the limb of the star.

The above approximation can be used to derive an analytic expression for the ratio of the mean intensity to the central intensity. The mean intensity I_mis the integral of the intensity over the disk of the star divided by the solid angle subtended by the disk:

ここで、Ωは観測者から星の外縁への角度である。
上の近似は、中央の放射強度に対する平均強度比の解析的表現を導出するために用いることができる。平均強度 I_mは、星の円盤全体にわたって強度を積分したものを円盤に対する立体角で割ったものである。
 

where dω=sin(θ)dθdφ is a solid angle element and the integrals are over the disk: 0≤φ≤2π and 0≤θ≤Ω. Although this equation can be solved analytically, it is rather cumbersome. However, for an observer at infinite distance from the star, the above equation simplifies to:

ここで、dω=sin(θ)dθdφは立体角要素であり、積分は0≤φ≤2π and 0≤θ≤Ωの円盤全体である。この式は解析的に解くことができるが、それはかなり取り扱いにくい。しかしながら、星から無限に離れた観測者である場合、上記の式は以下のように簡略化される。

---

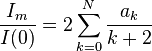
訳者注

†１）　ランバーチャンは黒体放射の場合に適用されるランバートのコサインの法則　I(ψ) = I₀cos(ψ) で放射面の法線方向からの観測者の角度ψによって放射強度が小さくなるという法則が適用できる放射物体のことを指す。ψが大きくなると観測される面の面積もcos(ψ)で小さくなるので、見た目の明るさ（放射強度/見た目の面積）は変わらないことになる。つまり、写真などで放射体の放射光を撮影した場合、どのような角度から撮影しても写真に写る放射体の明るさは変わらない。もし、太陽が黒体放射であった場合ランバーチャンとなるので、太陽のどの点も同じ明るさで観測されることになり、外縁暗光は起こらない。しかし、実際には外縁暗光が起こっているので、太陽は黒体放射ではないということになる。

†2）　透過度Tは入射光 I₀に対する透過光 I_t　の比で表され、光学的深さ(optical depth)をτとすると、
             T = I_t/ I₀= e^-τ
　　　　τ = σnl
で表される。ここで、σは吸収断面積、ｎは数密度、l は透過距離である。
τ＝１の場合、T = 1/e となり、透過光は3分の1近くになり、3分の2近くの大半の光は吸収されてしまう。このときの透過距離 l = 1 /σn が単位１のoptical depth（光学的深さ）に対応する距離になる。なかなか紛らわしいが、optical depthと透過距離が密接に関係している。

---

参考文献　Neckel, H. and Labs, D. (1994). "Solar Limb Darkening 1986-1990".Solar Physics153(1-2): 91–114.
の訳を試みる。

太陽外縁暗光1986-1990　（λλ303 to 1099nm)

abstract: 太陽活動が極小の1986年から極大の1990年までの太陽外縁暗光を繰り返し観測した。系統的変動は、瞬間的活発化そして太陽周期における位相の両方もしくはどちらかに依存していた可能性があるが、連続体波長および２つのブロードバンドのスペクトル間隔においても計測できなかった。完全に不規則な変動は、個々の連続的スキャン（粗い粒子化などによる）だけではなく、１日毎や季節毎の平均と関係しているが、通常１％以内であるが、しばしば２％もしくはそれ以上になることがある。マイナーな東-西非対称性は、季節平均においてさえも、おもにλ < 400 nm において、確立しているように見える。最終的な平均の外縁暗光係数は、Pierce and Slaughter(1977), Pierce, Slaughter, and Weiberger(1977)によって公表されたものと基本的には一致しているが、波長に対してプロットするとかなり小さな散乱を示している。

序論

ここ２０年ほどの太陽放射測定の新技術や測定感度の上昇に恵まれて、全太陽放射量の変化に関する研究は重要であり、そして将来有望な太陽物理の中の分野になった。すなわち、全太陽照射量は継続的に宇宙空間（Nimbus-7およびSMM衛星）で1978年から監視されている。現在、１太陽周期において規則的に約0.15％程度変化し、0.3％までのピークからピークへの強度の短期的揺動（Frohlich 1994を身よ）を示すことが知られている。