naga:5-1 > 5-6

SICP

naga

Exercise 5.1

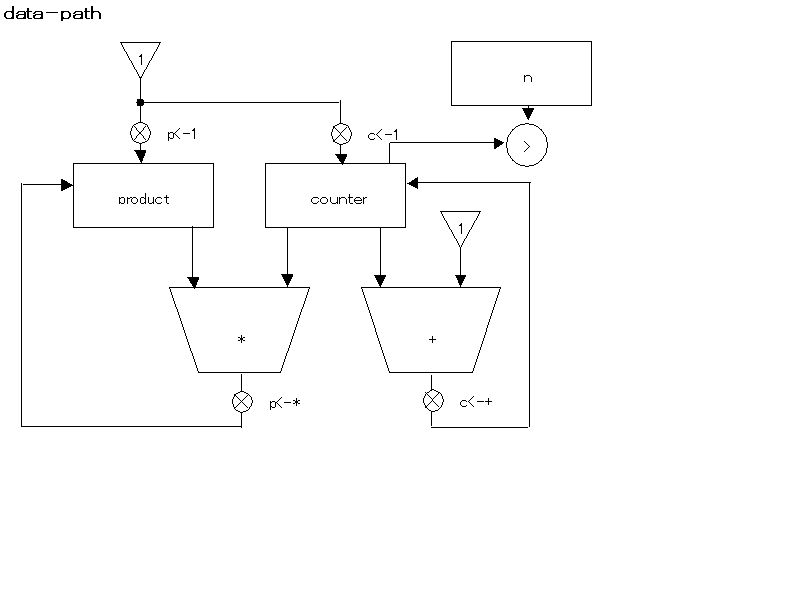
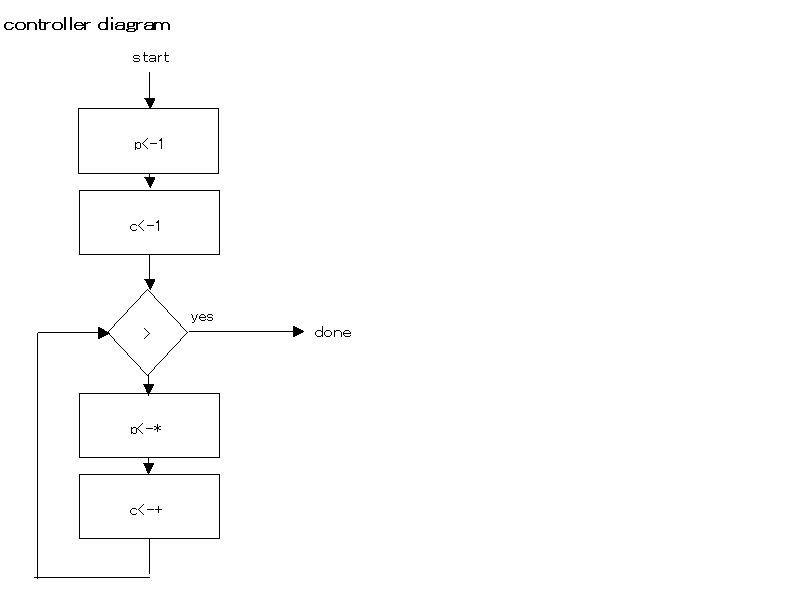
Exercise 5.2

(controller
   (assign product (const 1))
   (assign counter (const 1))
 test-counter
   (test (op >) (reg counter) (reg n))
   (branch (label fact-done))
   (assign product (op *) (reg product) (reg counter))
   (assign counter (op +) (reg counter) (const 1))
   (goto (label test-counter))
 fact-done)

Exercise 5.3

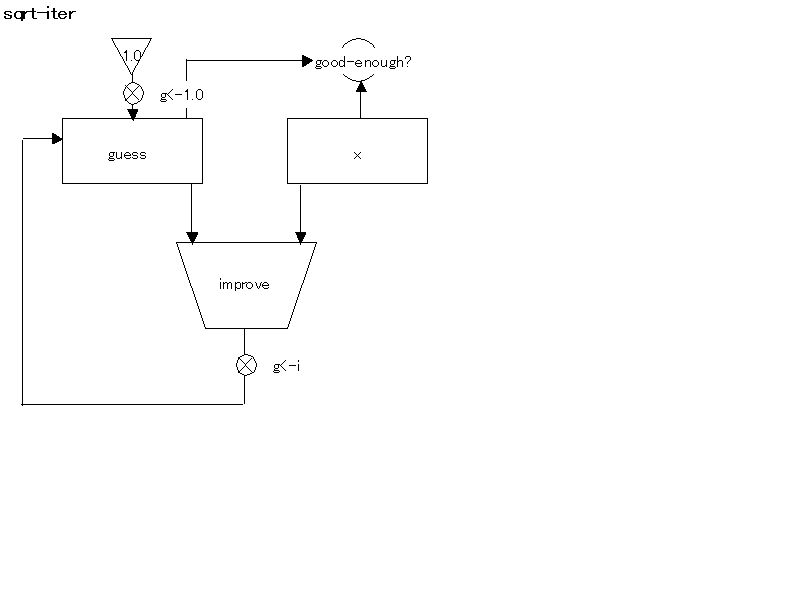
;;; good-enough? & improve are primitives
(controller
    (assign guess (const 1.0))
  test-guess
    (test (op good-enough?) (reg guess) (reg x))
    (branch (label sqrt-done))
    (assign guess (op improve) (reg guess) (reg x))
    (goto (label test-guess))
  sqrt-done)

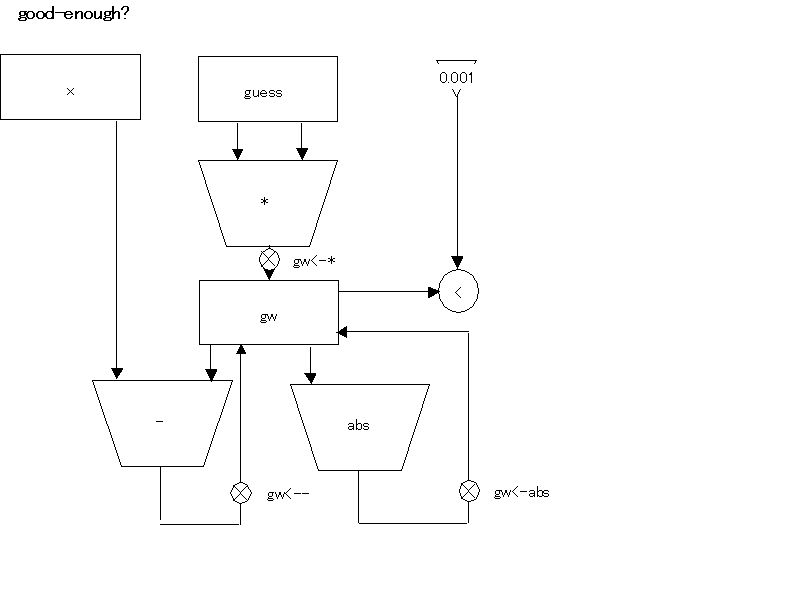
;;; improve is primitive
(controller
    (assign guess (const 1.0))
  test-guess
    ;;(test (op good-enough?) (reg guess) (reg x))
      (assign gw (op *) (reg guess) (reg guess))
      (assign gw (op -) (reg gw) (reg x))
      (assign gw (op abs) (reg gw))
      (test (op >) (reg gw) (const 0.001))
    (branch (label sqrt-done))
    (assign guess (op improve) (reg guess) (reg x))
    (goto (label test-guess))
  sqrt-done)

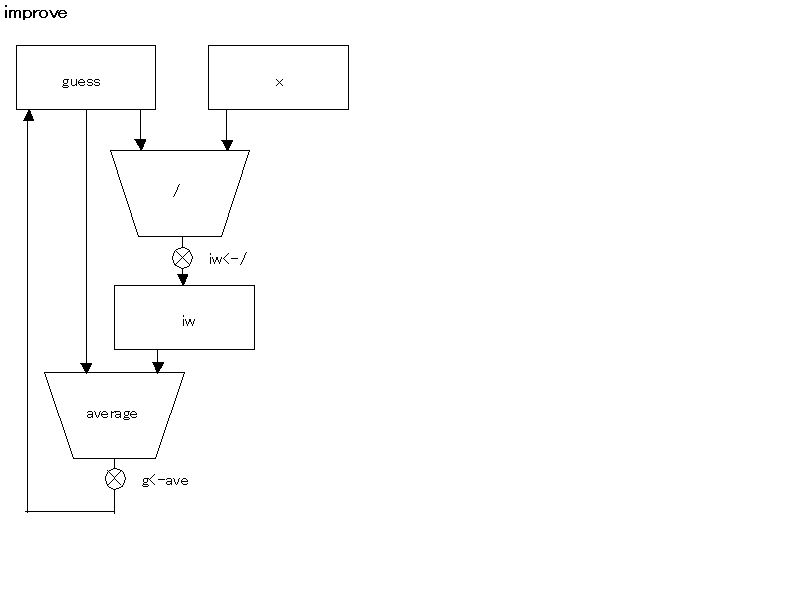
;;; controller
(controller
    (assign guess (const 1.0))
  test-guess
    ;;(test (op good-enough?) (reg guess) (reg x))
      (assign gw (op *) (reg guess) (reg guess))
      (assign gw (op -) (reg gw) (reg x))
      (assign gw (op abs) (reg gw))
      (test (op >) (reg gw) (const 0.001))
    (branch (label sqrt-done))
    ;;(assign guess (op improve) (reg guess) (reg x))
      (assign iw (op /) (reg guess) (reg x))
      (assign guess (op average) (reg guess) (reg iw)) 
    (goto (label test-guess))
  sqrt-done)

Exercise 5.4

a

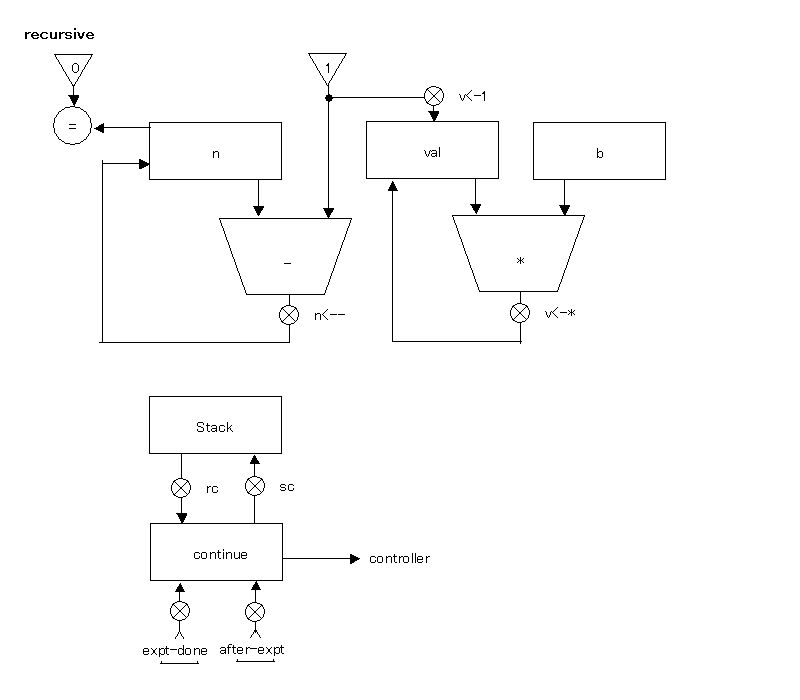
;;(define (expt b n)
;;  (if (= n 0)
;;      1
;;      (* b (expt b (- n 1)))))
(controller
 (assign continue (label expt-done))
 expt-loop
 (test (op =) (reg n) (const 0))
 (branch (label immediate-answer))
 (save continue)
 (assign continue (label afterexpt))
 (assign n (op -) (reg n) (const 1))
 (goto (label expt-loop))
 afterexpt
 (restore continue)
 (assign val (op *) (reg b) (reg val))
 (goto (reg continue))
 immediate-answer
 (assign val (const 1))
 (goto (reg continue))
 expt-done)
b

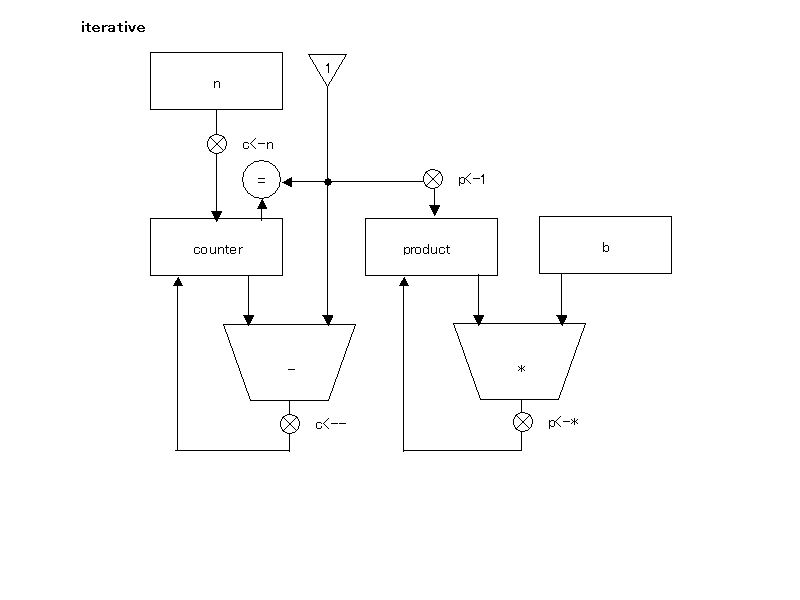
;;(define (expt b n)
;;  (define (expt-iter counter product)
;;    (if (= counter 0)
;;        product
;;        (expt-iter (- coutner 1) (* b product))))
;;  (expt-iter n 1))
(controller
 (assign counter (reg n))
 (assign product (const 1))
 expt-loop
 (test (op =) (reg counter) (const 0))
 (branch (label expt-done))
 (assign counter (op -) (reg counter) (const 1))
 (assign product (op *) (reg b) (reg product))
 (goto (label expt-loop))
 expt-done)

Exercise 5.5

;;; factorial
  (controller
     (assign continue (label fact-done))     ; set up final return address
   fact-loop
     (test (op =) (reg n) (const 1))
     (branch (label base-case))
     ;; Set up for the recursive call by saving n and continue.
     ;; Set up continue so that the computation will continue
     ;; at after-fact when the subroutine returns.
a)   (save continue)
b)   (save n)
     (assign n (op -) (reg n) (const 1))
     (assign continue (label after-fact))
     (goto (label fact-loop))
   after-fact
c)   (restore n)
d)   (restore continue)
e)   (assign val (op *) (reg n) (reg val))   ; val now contains n(n - 1)!
     (goto (reg continue))                   ; return to caller
   base-case
f)   (assign val (const 1))                  ; base case: 1! = 1
     (goto (reg continue))                   ; return to caller
   fact-done)
;;; n=3 時の a),b),c),d),e),f) の stack と val の様子
a) ((label fact-done))  (?)
b) (3 (label fact-done))  (?)
a) ((label fact-after) 3 (label fact-done))  (?)
b) (2 (label fact-after) 3 (label fact-done))  (?)
f) (2 (label fact-after) 3 (label fact-done))  (1)
c) ((label fact-after) 3 (label fact-done)) (1)
d) (3 (label fact-done))  (1)
e) (3 (label fact-done))  (2)
c) ((label fact-done))  (2)
d) () (2)
e) () (6)

;;; fibonacci
  (controller
     (assign continue (label fib-done))
   fib-loop
     (test (op <) (reg n) (const 2))
     (branch (label immediate-answer))
     ;; set up to compute Fib(n - 1)
a)   (save continue)
     (assign continue (label afterfib-n-1))
b)   (save n)                           ; save old value of n
c)   (assign n (op -) (reg n) (const 1)); clobber n to n - 1
     (goto (label fib-loop))            ; perform recursive call
   afterfib-n-1                         ; upon return, val contains Fib(n - 1)
d)   (restore n)
e)   (restore continue)
     ;; set up to compute Fib(n - 2)
f)   (assign n (op -) (reg n) (const 2))
g)   (save continue)
     (assign continue (label afterfib-n-2))
h)   (save val)                         ; save Fib(n - 1)
     (goto (label fib-loop))
   afterfib-n-2                         ; upon return, val contains Fib(n - 2)
i)   (assign n (reg val))               ; n now contains Fib(n - 2)
j)   (restore val)                      ; val now contains Fib(n - 1)
k)   (restore continue)
l)   (assign val                        ;  Fib(n - 1) +  Fib(n - 2)
             (op +) (reg val) (reg n)) 
     (goto (reg continue))              ; return to caller, answer is in val
   immediate-answer
m)   (assign val (reg n))               ; base case:  Fib(n) = n
     (goto (reg continue))
   fib-done)
;;; n=3 時の a),b),c),d),e),f),g),h),i),j),k),l),m) の stack val と n の様子
a) ((label fib-done))  (?)  (3)
b) (3 (label fib-done))  (?)  (3)
c) ((3) (label fib-done))  (?)  (2)
a) ((label afterfib-n-1) 3 (label fib-done))  (?)  (2)
b) (2 (label afterfib-n-1) 3 (label fib-done))  (?)  (2)
c) (2 (label afterfib-n-1) 3 (label fib-done))  (?)  (1)
m) (2 (label afterfib-n-1) 3 (label fib-done))  (1)  (1)
d) ((label afterfib-n-1) 3 (label fib-done))  (1)  (2)
e) (3 (label fib-done))  (1)  (2)
f) (3 (label fib-done))  (1)  (0)
g) ((label afterfib-n-1) 3 (label fib-done))  (1)  (0)
h) (1 (label afterfib-n-1) 3 (label fib-done))  (1)  (0)
m) (1 (label afterfib-n-1) 3 (label fib-done))  (0)  (0)
i) (1 (label afterfib-n-1) 3 (label fib-done))  (0)  (0)
j) ((label afterfib-n-1) 3 (label fib-done))  (1)  (0)
k) (3 (label fib-done))  (1)  (0)
l) (3 (label fib-done))  (1)  (0)
d) ((label fib-done))  (1)  (3)
e) ()  (1)  (3)
f) ()  (1)  (1)
g) ((label fib-done))  (1)  (1)
h) (1 (label fib-done))  (1)  (1)
m) (1 (label fib-done))  (1)  (1)
i) (1 (label fib-done))  (1)  (1)
j) ((label fib-done))  (1)  (1)
k) ()  (1)  (1)
l) ()  (2)  (1)

Exercise 5.6

;;; 下の←の２ヶ所
(controller
   (assign continue (label fib-done))
 fib-loop
   (test (op <) (reg n) (const 2))
   (branch (label immediate-answer))
   ;; set up to compute Fib(n - 1)
   (save continue)
   (assign continue (label afterfib-n-1))
   (save n)                           ; save old value of n
   (assign n (op -) (reg n) (const 1)); clobber n to n - 1
   (goto (label fib-loop))            ; perform recursive call
 afterfib-n-1                         ; upon return, val contains Fib(n - 1)
   (restore n)
   (restore continue)                 ; ← これと
   ;; set up to compute Fib(n - 2)
   (assign n (op -) (reg n) (const 2))
   (save continue)                    ; ← これ
   (assign continue (label afterfib-n-2))
   (save val)                         ; save Fib(n - 1)
   (goto (label fib-loop))
 afterfib-n-2                         ; upon return, val contains Fib(n - 2)
   (assign n (reg val))               ; n now contains Fib(n - 2)
   (restore val)                      ; val now contains Fib(n - 1)
   (restore continue)
   (assign val                        ;  Fib(n - 1) +  Fib(n - 2)
           (op +) (reg val) (reg n)) 
   (goto (reg continue))              ; return to caller, answer is in val
 immediate-answer
   (assign val (reg n))               ; base case:  Fib(n) = n
   (goto (reg continue))
 fib-done)