統計調査法～正規分布～正規分布表の使い方 - 小西研究室@電脳工房ＭＳＣ

第15回．統計調査法～正規分布～正規分布表の使い方

配布資料に基づいて説明します。

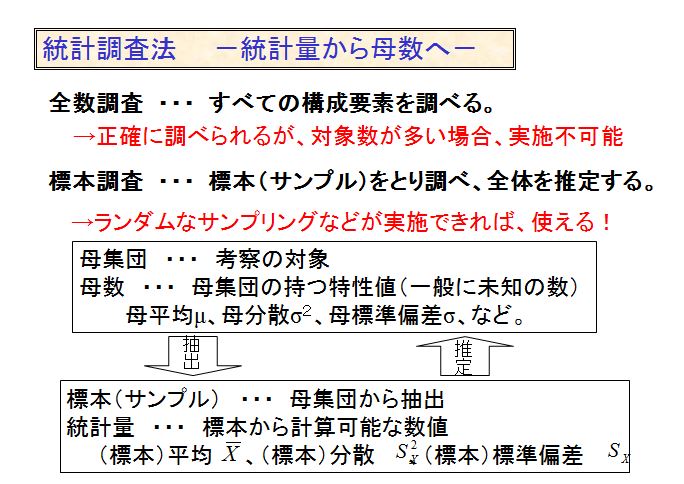
まず、社会調査には全数調査と標本調査があり、全数調査は現実的に実施不可能な場合が多く、
普通は、標本調査を行う。
アンケート調査や心理実験などが標本調査の実例といえる。

標本調査で得られたデータから、基本的な統計量を計算する。
統計的推定や統計的検定の手法を用いて、これらの統計量から「未知の母数」を推定する。

統計的推定や統計的検定の理論は「正規分布」が基本となって構成される。
度数分布表から作られたヒストグラムの長方形は、長方形全体の面積を１（=100%)とすると、
１つの長方形の面積が相対度数になることがわかる。

例えば、大学生の身長データから」ヒストグラムを作ってみる。

今回のテキストの巻末にも正規分布表が付録で収録されている。
この表は、左側が「整数.小数第1位」で上の欄が「小数第2位」を示す。
そして、「その値よりも大きい部分の面積（確率）」が表の中に書かれている。

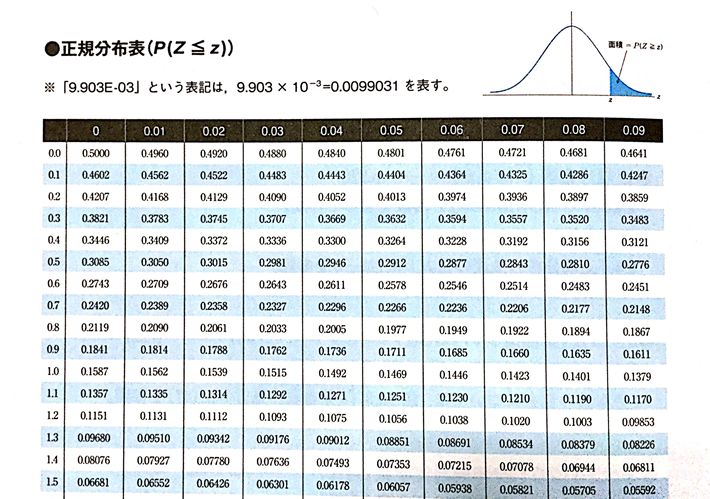
例えば、P{x≧1.23｝の値が知りたければ、左側で「1.2」上で「0.03」を選び、その位置に該当する
数値「0.1093」が対応する確率の値になっている。

P{－∞＜ｘ＜∞｝＝1.0（＝100％）

端から端まで、すべての確率は1.0である。
また、標準正規分布の場合には平均が０で中央に位置し、中央で左右対称形なので、

P{x≦０｝＝P{ｘ≧０｝＝0.5　となる。

【解答例】

(1).P{－1.2≦z≦1.0}=P{－1.2≦z≦0}+P{0≦z≦1.0}
　　　　　　　　　=P{0≦z≦1.2}+P{0≦z≦1.0} （対称性から）
　　　　　　　　　=(0.5P{z≧1.2})+(0.5－P{z≧1.0})
　　　　　　　　　=(0.5－0.1151)+(0.5－0.1587)
　　　　　　　　　=0.3849+0.3413=0.7262　　　■
(2).P{z≧1.5}=0.06681 （表の値そのまま） ■
(3).P{0≦z≦1.5}=0.5－P{z≧1.5}=0.5－0.06681＝0.43319＝0.4332　　■

次の定理が、標準正規分布（正規分布表が使える）と一般の正規分布（正規分布表は無い）を結びつける。

この定理から、すべての場合が計算できるようになる。

例えば、次の問題も解くことができる。

【例題1・解答例】

入学試験の成績xは平均73、標準偏差10の正規分布 $N(73,10^2)$ に従っている。
このため上の定理より、 $z=(x-73)/10$ とおくと、zは正規分布 $N(0,1^2)$ に従うことになる。
また、上の置き換えより、 $x=10z+73$ となる。
zは正規分布表を用いることができ、求める確率はP{x≧80}であるので、
　x≧80　⇔　10z+73≧80　⇔　10z≧7　⇔　z≧0.7
より、
P{x≧80}=P{z≧0.7}=0.2420
受験生が150名なので、
150×0.2420＝36.3
より、約36名いると予測できる。　　■

【例題2・解答例】

合格者が25名で、その確率は25÷150＝0.1667である。
正規分布表から、この値に近いzを探すと、0.97であることがわかる。

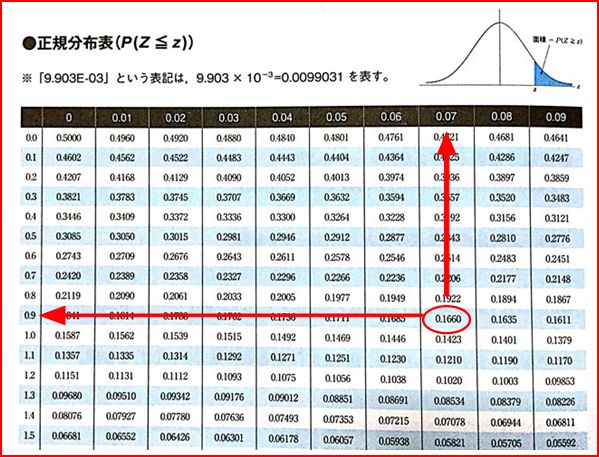
すなわち、P{z≧0.97}=0.1660である。
　x≧82.7　⇔　10z+73≧73+9.7=82.7　⇔　10z≧9.7　⇔　z≧0.97
より、成績xは82.7以上になるので、83点以上が合格になる。　　■

さらに、以下の問題は今後の基本になる。

【練習問題1・解答例】

仮定より試験の成績xは平均55、標準偏差15の正規分布 $N(55,15^2)$ に従っている。
このため上の定理より、 $z=(x-55)/15$ とおくと、zは正規分布 $N(0,1^2)$ に従うことになる。
また、上の置き換えより、 $x=15z+55$ となる。
「優」の学生の割合は0.15である。
正規分布表から、この値に近いzを探すと、1.035であることがわかる。
すなわち、P{z≧1.035}=0.15である。
　x≧70.525　⇔　15z+55≧55+15.525=70.525　⇔　15z≧10.35×15＝15.525　⇔　z≧1.035
より、成績xは70.525以上になるので、71点以上が合格になる。　　■

【練習問題2・解答例】

仮定より知能指数xは平均100、標準偏差15の正規分布 $N(100,15^2)$ に従っている。
このため上の定理より、 $z=(x-100)/15$ とおくと、zは正規分布 $N(0,1^2)$ に従うことになる。
また、上の置き換えより、 $x=15z+100$ となる。
zは正規分布表を用いることができ、求める確率はP{x≧150}であるので、
　x≧150　⇔　15z+100≧150　⇔　15z≧50　⇔　z≧3.33
より、
P{x≧150}=P{z≧3.33}=4.342E-04=0.0004342
よって、約0.043％占めると予測できる。　　■

【練習問題3・解答例】

(1).仮定よりxは平均5、標準偏差2の正規分布 $N(5,2^2)$ に従っている。
このため上の定理より、 $z=(x-5)/2$ とおくと、zは正規分布 $N(0,1^2)$ に従うことになる。
また、上の置き換えより、 $x=2z+5$ となる。
zは正規分布表を用いることができ、求める確率はP{x≦7}であるので、
　x≦7　⇔　2z+5≦7　⇔　2z≦2　⇔　z≦1
より、
P{x≦7}=P{z≦1}=1.0－P{z≧1}＝1.0－0.1587＝0.8413　　　■

(2).仮定より仮定よりxは平均μ、標準偏差σの正規分布 $N(\mu,\sigma^2)$ に従っている。
このため上の定理より、 $z=(x-\mu)/\sigma$ とおくと、zは正規分布 $N(0,1^2)$ に従うことになる。
また、上の置き換えより、 $x=\sigma z+\mu$ となる。
zは正規分布表を用いることができる。
まず、P{x≧6}=1－P{x≦6}=1-0.9773=0.0227
　x≧6　⇔　 $\sigma z+\mu$ ≧6　⇔　 $\sigma z$ ≧ $6-\mu$ 　⇔　z≧ $(6-\mu)/\sigma$
より、
$(6-\mu)/\sigma$ ＝2.0
が分かり、
$\mu+2\sigma=6$ ・・・①
また、同様に、
まず、P{x≧4}=1－P{x≦4}=1-0.8413=0.1587
　x≧4　⇔　 $\sigma z+\mu$ ≧4　⇔　 $\sigma z$ ≧ $4-\mu$ 　⇔　z≧ $(4-\mu)/\sigma$
より、
$(4-\mu)/\sigma$ ＝1.0
が分かり、
$\mu+\sigma=4$ 　・・・②
上の①②より、 $\sigma=2$ 、 $\mu=2$ 、がわかる。　　　■

質問や感想があればどうぞ。

何でも良いので質問して下さい。とにかく計算問題ができるように、練習をしておいてください。 -- 小西 (2015-07-13 14:23:18)
8月4日のアクセス件数が100でした。私も数回見ましたが、試験の前日でそこそこの訪問者が居て良かったです。正規分布の問題はとにかく図を描くことです。何の確率を求めるかが分かれば、あとは計算だけです。 -- 小西 (2015-08-05 01:41:55)

「統計調査法～正規分布～正規分布表の使い方」をウィキ内検索

最終更新：2015年08月05日 01:41

名前:
コメント: