この記事は
Competitive Programming Advent Calendar Div2013 の13日目の記事です。
競プロにおいて、文字列関連の問題への解法は、ローリングハッシュだのManacherだのKMPだのZだのTrieだのSuffix Arrayだの、色々なアルゴリズム・データ構造を使います。今回はその中でSuffix Automatonを取り上げたいと思います。
Suffix AutomatonはSuffix AutomataとかDAWG(Directed Acyclic Word Graph)とかの名前で呼ばれることもあるデータ構造です。一言で言ってしまえば、"Suffix Treeのノードをまとめたもの", "文字列Tのすべての連続部分文字列を受理するオートマトン"ですが、色々便利な性質を持っています。ですが、Suffix Automatonそのものについてほとんど資料がないのと、使わなければいけない問題が中ボス・ラスボス級の問題しかないため、あまり知名度がないと思っています。今回はSuffix Automatonの立ち位置・構築法・性質・実際の問題での使い方を書きます。
以後、特に断りのない限り、対象としている文字列をT, Tの長さをN, Tの文字の種類数をK(英小文字のみならK=26)としておきます。
立ち位置
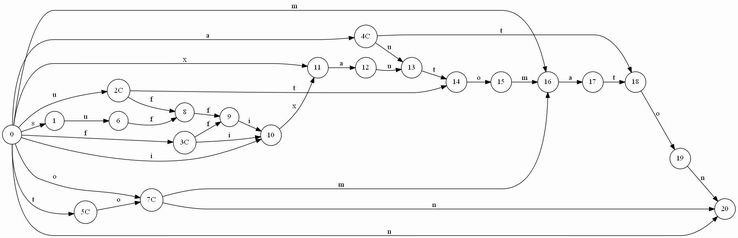
まず、同じ文字列に対して色々なデータ構造を構築した図を置きます。
KMPテーブル
+
...
Suffix Array
+
...
Suffix Tree
+
...
Suffix Tree(Suffix Linkつき)
+
...
Compressed Suffix Tree
+
...
Suffix Automaton
+
...
Suffix Automaton(Suffix Linkつき)
+
...
Compressed Suffix Automaton
+
...
Suffix AutomatonもSuffix Treeも、ノード0から文字列Tのすべての連続部分文字列(substring)をたどれます。Suffix Treeはノード数が
になってしまうので、競プロではあまり使えないデータ構造ですが、これをただまとめただけで、ノード数が
に落ちます。遷移を文字1個から複数文字列にした圧縮法でCompressed Suffix Treeになり、ノードをまとめるとSuffix Automatonになります。ちなみに両方とも圧縮するということも出来て、Compressed Suffix AutomatonとかCDAWGとかいうのができます。こいつはよくわからないので名前だけ出しておきます。
構築法
実際に組みたいときは
e-maxxせんせの記事 の擬似コードをそのまんま実装すれば作れちゃいます。時間計算量O(Nlog K)の空間計算量O(N)です(Kは文字種類数). Suffix ArrayのO(N)構築法等に比べればぜんぜん難しくないので一度つくってみちゃいましょう。
Suffix Automatonのノードは以下のプロパティを持っています。t0はSuffix Automatonの初期ノードです。
len
t0からの最長距離。
link
Suffix Link. t0からそのノードAに至るパスの文字列を先頭から1文字ずつ削っていってまたt0からのパスを構成する時、はじめてA以外に至るノード。
next[c]
現在のノードから1文字cをたどって行く先のノード。
他に次のプロパティもあると嬉しいです。
isCloned
cloneしてできたノードかどうか。クローン元のノードを持っておいても良い。
id
トポロジカルオーダー。
key
そのノードに至る最後の文字。Suffix Automatonではノードの入次辺は全部同じ文字になるため、実装次第ではノードにまとめたほうが良い場合もある。
以下引用の範囲をこえた擬似コード…
+
...
struct state {
int len, link ;
map < char , int > next ;
} ;
const int MAXLEN = 100000 ;
state st [ MAXLEN * 2 ] ;
int sz, last ;
void sa_init ( ) {
sz = last = 0 ;
st [ 0 ] . len = 0 ;
st [ 0 ] . link = - 1 ;
++ sz ;
}
void sa_extend ( char c ) {
int cur = sz ++ ;
st [ cur ] . len = st [ last ] . len + 1 ;
int p ;
for ( p = last ; p ! = - 1 && ! st [ p ] . next . count ( c ) ; p = st [ p ] . link )
st [ p ] . next [ c ] = cur ;
if ( p == - 1 )
st [ cur ] . link = 0 ;
else {
int q = st [ p ] . next [ c ] ;
if ( st [ p ] . len + 1 == st [ q ] . len )
st [ cur ] . link = q ;
else {
int clone = sz ++ ;
st [ clone ] . len = st [ p ] . len + 1 ;
st [ clone ] . next = st [ q ] . next ;
st [ clone ] . link = st [ q ] . link ;
for ( ; p ! = - 1 && st [ p ] . next [ c ] == q ; p = st [ p ] . link )
st [ p ] . next [ c ] = clone ;
st [ q ] . link = st [ cur ] . link = clone ;
}
}
last = cur ;
}
この擬似コードでは1文字ずつ追加して対応するノードと辺を追加しています。擬似コードがなにをしているのかを簡単に書くと、
ノードt0を作成し、sourceとする。last=t0とする。
各文字に対して以下を繰り返す。 新しく来た文字をcとする。
とりあえず新しいノードcurをつくり、len(cur):=len(last)+1とする。
linkをたどって、訪れたノードすべてに対し、文字cでの行き先をcurとするようにnextを張る。これを、pathがt0で終わってしまうか、すでに文字cでの行き先が別なノードqになっている元ノードpがあるところで終わる。
(p,q)が存在する場合 len(q)=len(p)+1なら、以降linkをたどってもすでにqへのnextで埋まっているだろうから、新たに張りに行く必要がない。curのlinkをqに張って終了。
len(q)>len(p)+1なら、以降のlinkでもやはりqへのnextで埋まっているが、最長のもののlenがジャンプしていることになり、qはcurの代わりにはならないので、len(clone)=len(p)+1を満たすqのクローンcloneをつくり、cloneへの入次辺もすべてqと同じにする。qからclone, curからcloneにlinkを張って終了。
last:=curとする。
という感じです。作り終わった後、使うアルゴリズムに応じてトポロジカルソートやnext内部のソートをしたりしなかったりします。
各文字について独立な構築法のため、元の文字列が文字木でも同様につくれるっぽいです。この場合lastがsinkとは限らないため、curをつくったけどいきなり(p,q)があって、curそのものが要らなかったみたいな場合があるので注意です。
構築時に注意すること
まずcloneのクローニングはディープコピーです。ひとつでもコピーし忘れるとおかしくなります。
次に、mapについて。この構築法をO(Nlog K)たらしめているのは、ノードのプロパティnextのmapが二分探索木であることです。このnextの実装をどうするかで構築速度にかなり差が出てきます。このmapに要求されることは、
挿入・取得が高速にできること。
全走査が楽に書けること。
全mapを合わせても要素数が3N-3以下しかないことがわかっているため、少ない要素数のmapが大量に並ぶ状態を高速に作成できること。
(ソートが楽に書けること。)
です。2番目の性質は、DPを組んだ時に全走査のコードを書きますが、mapを複雑な構成にすると全走査のコードも比例して複雑になるケースがあり、書きづらくなってしまいます。また3番目の性質については、ほとんどの文字列で半分以上のノードのnextが要素数1になるので、無視できません。
以前擬似コードだけ見てつくったときは、nextは26要素の配列だったのですが、元の文字列が
文字になるとJavaではメモリを300MB近く使ってしまいます。色々試した結果、自分の実装では、動的に要素数がふえる配列と、文字包含判定をbitで判定できるようなintを組み合わせています。文字種類数が64以上,2以下になると構造を変えたほうがパフォーマンスがよくなると思います。
以下自分の構築部分。クラス名が荒ぶっているのは試行錯誤の結果です。
+
...
public class SuffixAutomatonNew4Hashed {
public Node t0;
public int len;
public Node[ ] nodes;
public int gen;
private SuffixAutomatonNew4Hashed( int n)
{
gen = 0 ;
nodes = new Node[ 2 * n] ;
this .t0 = makeNode( 0 , false ) ;
}
private Node makeNode( int len, boolean isCloned)
{
Node node = new Node( ) ;
node.id = gen;
node.isCloned = isCloned;
node.len = len;
nodes[ gen++ ] = node;
return node;
}
public static class Node
{
public int id;
public int len;
public char key;
public Node link;
private Node[ ] next = new Node[ 3 ] ;
public boolean isCloned;
public int np = 0 ;
public int hit = 0 ;
public void putNext( char c, Node to)
{
to.key = c;
if ( hit<< 31 - ( c- 'a' ) < 0 ) {
for ( int i = 0 ; i < np; i++ ) {
if ( next[ i] .key == c) {
next[ i] = to;
return ;
}
}
}
hit |= 1 << c- 'a' ;
if ( np == next.length ) {
next = Arrays copyOf ( next, np* 2 ) ;
}
next[ np++ ] = to;
}
public boolean containsKeyNext( char c)
{
return hit<< 31 - ( c- 'a' ) < 0 ;
// for(int i = 0;i < np;i++){
// if(next[i].key == c)return true;
// }
// return false;
}
public Node getNext( char c)
{
if ( hit<< 31 - ( c- 'a' ) < 0 ) {
for ( int i = 0 ; i < np; i++ ) {
if ( next[ i] .key == c) return next[ i] ;
}
}
return null ;
}
}
public static SuffixAutomatonNew4Hashed build( char [ ] str)
{
int n = str.length ;
SuffixAutomatonNew4Hashed sa = new SuffixAutomatonNew4Hashed( n) ;
sa.len = str.length ;
Node last = sa.t0 ;
for ( char c : str) {
last = sa.extend ( last, c) ;
}
return sa;
}
public Node extend( Node last, char c)
{
Node cur = makeNode( last.len + 1 , false ) ;
Node p;
for ( p = last; p != null && ! p.containsKeyNext ( c) ; p = p.link ) {
p.putNext ( c, cur) ;
}
if ( p == null ) {
cur.link = t0;
} else {
Node q = p.getNext ( c) ; // not null
if ( p.len + 1 == q.len ) {
cur.link = q;
} else {
Node clone = makeNode( p.len + 1 , true ) ;
clone.next = Arrays copyOf ( q.next , q.next .length ) ;
clone.hit = q.hit ;
clone.np = q.np ;
clone.link = q.link ;
for ( ; p != null && q.equals ( p.getNext ( c) ) ; p = p.link ) {
p.putNext ( c, clone) ;
}
q.link = cur.link = clone;
}
}
return cur;
}
public SuffixAutomatonNew4Hashed lexSort( )
{
for ( int i = 0 ; i < gen; i++ ) {
Node node = nodes[ i] ;
Arrays sort ( node.next , 0 , node.np , new Comparator< Node> ( ) {
public int compare( Node a, Node b) {
return a.key - b.key ;
}
} ) ;
}
return this ;
}
public SuffixAutomatonNew4Hashed sortTopologically( )
{
int [ ] indeg = new int [ gen] ;
for ( int i = 0 ; i < gen; i++ ) {
for ( int j = 0 ; j < nodes[ i] .np ; j++ ) {
indeg[ nodes[ i] .next [ j] .id ] ++;
}
}
Node[ ] sorted = new Node[ gen] ;
sorted[ 0 ] = t0;
int p = 1 ;
for ( int i = 0 ; i < gen; i++ ) {
Node cur = sorted[ i] ;
for ( int j = 0 ; j < cur.np ; j++ ) {
if ( -- indeg[ cur.next [ j] .id ] == 0 ) {
sorted[ p++ ] = cur.next [ j] ;
}
}
}
for ( int i = 0 ; i < gen; i++ ) sorted[ i] .id = i;
nodes = sorted;
return this ;
}
public String ( )
{
StringBuilder sb = new StringBuilder( ) ;
for ( Node n : nodes) {
if ( n != null ) {
sb.append ( String format ( "{id:%d, len:%d, link:%d, cloned:%b, " ,
n.id ,
n.len ,
n.link != null ? n.link .id : null ,
n.isCloned ) ) ;
sb.append ( "next:{" ) ;
for ( int i = 0 ; i < n.np ; i++ ) {
sb.append ( n.next [ i] .key + ":" + n.next [ i] .id + "," ) ;
}
sb.append ( "}" ) ;
sb.append ( "}" ) ;
sb.append ( "\n " ) ;
}
}
return sb.toString ( ) ;
}
}
デバッグについて
Suffix Automatonは頂点・辺ラベルつきDAGなので、きちんと作れているかとか遷移がどうなっているかを確認したいときは図示するのが非常に効果的です。graphvizにコピペして直接図をつくれるような文字列(DOT言語)を吐く関数とか、
Google Chart API に投げる用の関数を用意しておくと良いと思います。
+
...
public String ( Node n)
{
if ( n.isCloned ) {
return n.id + "C" ;
} else {
return n.id + "" ;
}
}
public String ( boolean next, boolean suffixLink)
{
StringBuilder sb = new StringBuilder( "digraph{\n " ) ;
sb.append ( "graph[rankdir=LR];\n " ) ;
sb.append ( "node[shape=circle];\n " ) ;
for ( Node n : nodes) {
if ( n != null ) {
if ( suffixLink && n.link != null ) {
sb.append ( "\" " + label( n) + "\" " )
.append ( "->" )
.append ( "\" " + label( n.link ) + "\" " )
.append ( "[style=dashed];\n " ) ;
}
if ( next && n.next != null ) {
for ( int i = 0 ; i < n.np ; i++ ) {
sb.append ( "\" " + label( n) + "\" " )
.append ( "->" )
.append ( "\" " + label( n.next [ i] ) + "\" " )
.append ( "[label=\" " )
.append ( n.next [ i] .key )
.append ( "\" ];\n " ) ;
}
}
}
}
sb.append ( "}\n " ) ;
return sb.toString ( ) ;
}
public String ( boolean next, boolean suffixLink)
{
StringBuilder sb = new StringBuilder( "http://chart.apis.google.com/chart?cht=gv:dot&chl=" ) ;
sb.append ( "digraph{" ) ;
for ( Node n : nodes) {
if ( n != null ) {
if ( suffixLink && n.link != null ) {
sb.append ( n.id )
.append ( "->" )
.append ( n.link .id )
.append ( "[style=dashed]," ) ;
}
if ( next && n.next != null ) {
for ( int i = 0 ; i < n.np ; i++ ) {
sb.append ( n.id )
.append ( "->" )
.append ( n.next [ i] .id )
.append ( "[label=" )
.append ( n.next [ i] .key )
.append ( "]," ) ;
}
}
}
}
sb.append ( "}" ) ;
return sb.toString ( ) ;
}
例
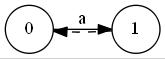
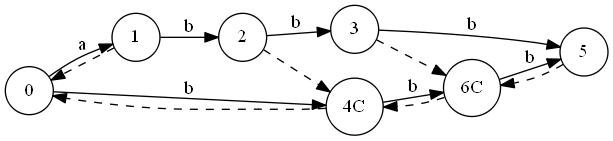
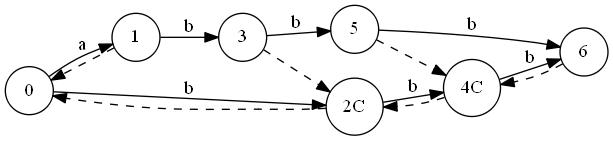
T="abbb"に対しSuffix Automatonを構築していく最中の図を置いておきます。ノードが追加されていくのと、最終的な形はトポロジカル順にはなっていないことに注目してみてください。"C"はクローンノードです。
"a"
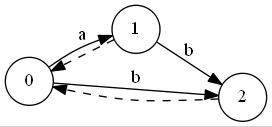
"ab"
"abb"
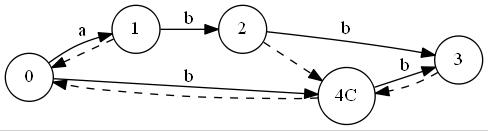
"abbb"
トポロジカルソートを行って
.
性質
これはかなり大事な項で、性質を知らないと未知の問題に対応できません・・
Suffix Automatonのノード数はたかだか2N-1個。("abbb...bb")
Suffix Automatonの有向辺数はたかだか3N-4個。("abbb...bc")
任意のclonedなノードxについて、x.original.link = xである。
ノードxは複数のsubstringに対応するが、それは下のように最短のものがベースとなり、そこの頭に1文字ずつ追加してできる感じの文字列の集合になっている。 ab
aab
aaab
caaab
これらの最長の長さはlen. t0からxへnextを通って行く最長経路長。
これらの最短の長さはlink.len+1. t0からxへnextを通って行く最短経路長。
これらのsubstringの出現箇所の末尾位置はすべて一致する。 初回出現位置は、xがclonedならx.original.len, clonedでなければ、x.len.
それ以外の出現位置は、xからlinkを逆向きにたどって到達するclonedでないノードたちのlenに相当する。そしてそれらが全てである(つまり到達した非clonedノードの個数+1を数えればsubstringの出現頻度がわかる)。
clonedなノードは、Tのprefixを含んでいない。逆に非clonedなノードは常に含んでいる。上記の例でabからbを持つnodeを求めたいときは、xからlinkをたどれば良い。 Suffix Treeが、文字列TのすべてのsubstringについてのTrieであることから、Suffix AutomatonをTrieのように使うことも出来ます。 t0からTとは別の文字列Uの文字をたどっていく場合、U[0,pos]に一致する最長のsuffixの長さ(suflen[pos])は、 nextをたどった場合、suflen[pos]=suflen[pos-1]+1.
linkを通ってからnextをたどった場合、たどった先のノードをdとして、suflen[pos]=d.len+1
linkを通ってt0にいきつき、さらにnextをたどれない場合、suflen[pos]=0
linkは、t0をsinkとする有向木を構成する。 アルゴリズム
e-maxxせんせの記事 の後半にはSuffix Automatonを使った色々なアルゴリズムが載っています。そこからいくつか。Suffix Automatonを使う問題では、最初の2個をおさえておけばなんとかなります。
Tに含まれる相異なるsubstringの個数を求める
これはt0を値1とし、そこから配るDPで配ったときの全体の合計-1です。-1は、t0の分(空文字列)です。あとで書きますが、逆向きのDPでも求められます。O(N). Suffix Array+LCPでも求められます。
+
...
public long numberOfDistinctSubstrings( ) {
long [ ] dp = new long [ gen] ;
dp[ 0 ] = 1 ;
long ret = 0 ;
for ( int i = 0 ; i < gen; i++ ) {
Node n = this .nodes [ i] ;
ret += dp[ i] ;
for ( int j = 0 ; j < n.np ; j++ ) {
dp[ n.next [ j] .id ] += dp[ i] ;
}
}
return ret- 1 ; // remove empty
}
Tの各substringについて、T内で何回出現するかを全列挙する
上記の逆DPパターンです。クローンされていないノードに1を割り当て、suffix linkにしたがって木をのぼっていくDPをします。求めたい文字列Uについて、Uをt0からたどっていきついたノードでの値が答えになります。O(N). t0での値が、先に書いた相異なるsubstringの個数になります。
クローンノードは言ってみれば便宜上のノード(qがcurのlink先としてふさわしくないから設けたノード)なので、カウントしないっぽいです。
+
...
public int [ ] enumNumberOfOccurrences( )
{
int n = gen;
int [ ] dp = new int [ n] ;
for ( int i = n- 1 ; i >= 1 ; i-- ) {
if ( ! nodes[ i] .isCloned ) dp[ i] ++;
dp[ nodes[ i] .link .id ] += dp[ i] ;
}
return dp;
}
Tに含まれる相異なるsubstringのうち、辞書順でk番目のものを答える
今度は全ノードに1を割り当てて、nextを使って逆向きにDPします。こうすると、各ノードでは、そのノード以降にたどって行けるノード、つまり相異なるsubstringの個数がわかります。これを利用して貪欲に辞書順k番目のものを求めることができます。
あらかじめnextをアルファベット昇順にソートして置かなければいけないので注意。 O(N).
+
...
public long [ ] preprocessDistinctSubstring( )
{
int n = gen;
// preprocess
long [ ] dp = new long [ n] ;
for ( int i = n- 1 ; i >= 0 ; i-- ) {
dp[ i] = 1 ;
Node node = nodes[ i] ;
for ( int j = 0 ; j < node.np ; j++ ) {
int toid = node.next [ j] .id ;
dp[ i] += dp[ toid] ;
}
}
return dp;
}
public String ( long K, long [ ] dp)
{
if ( K <= 0 ) return null ;
if ( K >= dp[ 0 ] ) return null ;
// greedy
Node cur = t0;
StringBuilder sb = new StringBuilder( ) ;
while ( K > 0 ) {
K--;
for ( int j = 0 ; j < cur.np ; j++ ) {
Node next = cur.next [ j] ;
int toid = next.id ;
if ( K- dp[ toid] < 0 ) {
sb.append ( next.key ) ;
cur = next;
break ;
} else {
K -= dp[ toid] ;
}
}
}
return sb.toString ( ) ;
}
TとUのLCS (Longest Common Substring:最長共通連続部分文字列)をひとつ求める
TをtrieとみてUで検索をかける感じです(引数がtになってますが・・)。現在までのsuffixの最大一致長が、link.len+1であることを覚えておけばわけないです。O(N).
+
...
public char [ ] lcs( char [ ] t)
{
if ( t.length == 0 ) return new char [ 0 ] ;
Node v = t0;
int l = 0 , best = 0 , bestPos = 0 ;
for ( int i = 0 ; i < t.length ; i++ ) {
while ( v != t0 && ! v.containsKeyNext ( t[ i] ) ) {
v = v.link ;
l = v.len ;
}
if ( v.containsKeyNext ( t[ i] ) ) {
v = v.getNext ( t[ i] ) ;
l++;
}
if ( l > best) {
best = l; bestPos = i;
}
}
return Arrays copyOfRange ( t, bestPos- best+ 1 , bestPos+ 1 ) ;
}
Tの各substringの初回出現位置を列挙する
探索するsubstringをQとし、t0からたどって行き着く先のノードをDとすると、Dがクローンされていないノードの場合は、len-|Q|がヒットする頭の位置(0-indexed)になります。クローンされたノードはオリジナルのノードのlen-|Q|でヒットします。オリジナルをたどれなくとも、トポロジカル降順にDPして最小をとればなんとかなったりします。
+
...
public int [ ] enumFirstOccurences( )
{
int [ ] fo = new int [ gen] ;
Arrays fill ( fo, Integer MAX_VALUE ) ;
for ( int i = gen- 1 ; i >= 0 ; i-- ) {
if ( ! nodes[ i] .isCloned ) {
fo[ i] = nodes[ i] .len ;
}
if ( i > 0 && nodes[ i] .link .isCloned && fo[ i] < fo[ nodes[ i] .link .id ] ) {
fo[ nodes[ i] .link .id ] = fo[ i] ;
}
}
return fo;
}
あるクエリQに対し、Tのすべての出現位置を列挙する
直接やればいいじゃんとか言われそうですが一応・・
出現回数を列挙するところで逆向きに木DPしていましたが、このsuffix link木をDFSでたどって非クローンノードのlenを集めると、出現位置を列挙できます。あらかじめsuffix linkの逆向きのグラフをつくっておかなければいけないので面倒くさいです。
+
...
public Node[ ] [ ] ilinks( )
{
int n = gen;
int [ ] ip = new int [ n] ;
for ( int i = 1 ; i < n; i++ ) ip[ nodes[ i] .link .id ] ++;
Node[ ] [ ] ilink = new Node[ n] [ ] ;
for ( int i = 0 ; i < n; i++ ) ilink[ i] = new Node[ ip[ i] ] ;
for ( int i = 1 ; i < n; i++ ) ilink[ nodes[ i] .link .id ] [ -- ip[ nodes[ i] .link .id ] ] = nodes[ i] ;
return ilink;
}
public Node track( char [ ] q)
{
Node cur = t0;
for ( char c : q) {
cur = cur.getNext ( c) ;
if ( cur == null ) return null ;
}
return cur;
}
public BitSet ( char [ ] q, Node[ ] [ ] ilinks)
{
BitSet = new BitSet ( ) ;
Node cur = track( q) ;
if ( cur == null ) return occurs;
dfsIndexOfAll( cur, q.length , ilinks, occurs) ;
return occurs;
}
private void dfsIndexOfAll( Node cur, int qlen, Node[ ] [ ] ilinks, BitSet )
{
if ( ! cur.isCloned ) bs.set ( cur.len - qlen) ;
for ( Node e : ilinks[ cur.id ] ) dfsIndexOfAll( e, qlen, ilinks, bs) ;
}
T内の極大長繰り返し文字列を全列挙する (12/24 修正)
runといい、ある周期iに対して、長さが2i以上ある周期iのTのsubstringで、それ以上のばすと周期iでなくなってしまうようなものすべてをさします。これの総数はO(N)なので、全列挙が可能です。
Tに対し、s-factorizationとかf-factorizationとかLempel-Ziv factorizationとかいう分割を行って、その仕切りにまたがるようなrunをすべて列挙します。これらは、仕切りにまたがらないようなrunを、位置を気にしなければすべて包含しているため、Tのなかでk回繰り返す最長substringは?とか、Tのなかで最大の繰り返し数を持つsubstringは?とかいう問題に対してはこれで十分対応できます。
s-factorizationは、現在のsegmentの文字列が、以前に出てきている限りsegmentを伸ばし続けるみたいな切り方で、
babbababbabba
だと、
b|a|b|bab|abbab|ba
みたいな切り方になります。これの隣接する2個のsegment
について、そこにまたがるrunの最長の長さは2(|u_{i-1}|+|u_i|)になるので、その長さだけ切り取ってやったあと、各周期iについて、仕切りの両側でその周期を実現する最長長LS,LPを求めてLS+LP>=iになっていれば(LP側に周期のある)runがいっちょあがりという概略です。LS側に周期のあるrunは探索方向を逆にしてLS,LPを作りなおして求められます。LSとLPはZ-algorithmで列挙できるので、全体でO(N)です。
なおs-factorizationはSuffix Arrayからも求めることができるらしいので(参考文献3)、今度はそれに挑戦してみたいです。
+
...
public int [ ] enumFirstOccurences( )
{
int [ ] fo = new int [ gen] ;
Arrays fill ( fo, Integer MAX_VALUE ) ;
for ( int i = gen- 1 ; i >= 0 ; i-- ) {
if ( ! nodes[ i] .isCloned ) {
fo[ i] = nodes[ i] .len ;
}
if ( i > 0 && nodes[ i] .link .isCloned && fo[ i] < fo[ nodes[ i] .link .id ] ) {
fo[ nodes[ i] .link .id ] = fo[ i] ;
}
}
return fo;
}
public int [ ] factor( char [ ] s, int [ ] fo)
{
int [ ] f = new int [ len+ 1 ] ;
int p = 0 ;
f[ p++ ] = 0 ;
Node cur = t0;
int llen = 0 ;
for ( int i = 0 ; i < len; i++ ) {
if ( i > 0 ) {
Node next = cur.getNext ( s[ i] ) ;
cur = next == null ? t0 : next;
}
while ( fo[ cur.id ] >= i+ 1 && cur.len >= llen+ 1 ) cur = cur.link ;
if ( cur.len <= llen) {
if ( llen == 0 ) {
if ( i+ 1 < len) f[ p++ ] = i+ 1 ;
llen = 0 ;
} else {
f[ p++ ] = i;
llen = 1 ;
}
} else {
llen++;
}
}
return Arrays copyOf ( f, p) ;
}
public int [ ] [ ] enumType1Runs( int [ ] f, char [ ] s)
{
Map< Long int [ ] > ret = new HashMap< Long int [ ] > ( ) ;
long H = 1000000009 ;
for ( int i = 0 ; i < f.length - 1 ; i++ ) {
int left = f[ i] , mid = f[ i+ 1 ] , right = i+ 2 < f.length ? f[ i+ 2 ] : s.length ;
int start = Math max ( 0 , left- ( right- left) ) ;
{
char [ ] t = new char [ mid- start+ right- start] ;
int tp = 0 ;
for ( int j = mid- 1 ; j >= start; j-- ) t[ tp++ ] = s[ j] ;
for ( int j = right- 1 ; j >= start; j-- ) t[ tp++ ] = s[ j] ;
int [ ] LS = Z( t) ;
char [ ] u = Arrays copyOfRange ( s, mid, right) ;
int [ ] LP = Z( u) ;
for ( int j = 0 ; j < right- mid; j++ ) {
int lpv = j+ 1 == right- mid ? 0 : LP[ j+ 1 ] ;
int lsv = Math min ( mid- start, LS[ ( mid- start) + ( right- mid) - 1 - j] ) ;
if ( lsv + lpv >= j+ 1 ) {
int L = mid- lsv, R = mid+ j+ lpv+ 1 , P = j+ 1 ;
long hash = ( L* H+ R) * H+ P;
if ( ! ret.containsKey ( hash) ) {
ret.put ( hash, new int [ ] { L, R, P} ) ; // {start,end,period}, [start,end)
}
}
}
}
{
char [ ] t = new char [ right- mid+ right- start] ;
int tp = 0 ;
for ( int j = mid; j < right; j++ ) t[ tp++ ] = s[ j] ;
for ( int j = start; j < right; j++ ) t[ tp++ ] = s[ j] ;
int [ ] LS = Z( t) ;
char [ ] u = new char [ mid- start] ;
int up = 0 ;
for ( int j = mid- 1 ; j >= start; j-- ) u[ up++ ] = s[ j] ;
int [ ] LP = Z( u) ;
for ( int j = 0 ; j < mid- start; j++ ) {
int lpv = j+ 1 == mid- start ? 0 : LP[ j+ 1 ] ;
int lsv = Math min ( right- mid, LS[ ( right- mid) + ( mid- start) - 1 - j] ) ;
if ( lsv + lpv >= j+ 1 ) {
int L = mid- j- lpv- 1 , R = mid+ lsv, P = j+ 1 ;
long hash = ( L* H+ R) * H+ P;
if ( ! ret.containsKey ( hash) ) {
ret.put ( hash, new int [ ] { L, R, P} ) ; // {start,end,period}, [start,end)
}
}
}
}
}
return ret.values ( ) .toArray ( new int [ 0 ] [ ] ) ;
}
public static int [ ] Z( char [ ] str)
{
int n = str.length ;
int [ ] z = new int [ n] ;
if ( n == 0 ) return z;
z[ 0 ] = n;
int l = 0 , r = 0 ;
for ( int i = 1 ; i < n; i++ ) {
if ( i > r) {
l = r = i;
while ( r < n && str[ r- l] == str[ r] ) r++;
z[ i] = r- l; r--;
} else {
int k = i- l;
if ( z[ k] < r- i+ 1 ) {
z[ i] = z[ k] ;
} else {
l = i;
while ( r < n && str[ r- l] == str[ r] ) r++;
z[ i] = r- l; r--;
}
}
}
return z;
}
"babbababbabba"に対して行った結果。[[a,b,c],x]は、x=T[a,b)が周期cのrunだよという意味です。
[[5, 13, 3], babbabba]
[[5, 11, 3], babbab]
[[3, 8, 2], babab]
[[10, 12, 1], bb]
[[0, 11, 5], babbababbab]
[[2, 4, 1], bb]
[[0, 6, 3], babbab]
パターンマッチ検索
パターンマッチ検索の分野ではSuffix Automatonを使った検索はよく使われていたみたいです(BDM, BNDM).
問題例 (12/24 追加)
Suffix Automatonを使わなければ解けないという問題は少ないですが、少ないなりに色々挙げます。やっつけ問題概要もあげておきます。
50000文字の文字列が与えられる。これの相異なるsubstringの総数を求めよ。
90000文字の文字列が与えられる。これの相異なるsubstringのうち辞書順でK番目に小さいものを求めよ。Kは500個与えられる。
100000文字の文字列A,Bが与えられるので、それぞれの相異なるsubstringの集合同士の、相異なる要素の個数を求めよ。
1000000文字の文字列Sと、100000個・合計1000000文字のクエリQ_iが与えられる。
各クエリQ_iについて、Q_iをrotateしてできる相異なる文字列のSでの出現個数の合計を求めよ。
+
...
Q_iを2個つなげて末尾1文字を削ると、rotateしてできる文字列がすべて長さ一定で含まれる文字列になるので、それでSのSuffix Automatonを検索します。至ったノードをマークしておき、マークしたノードでの"出現回数"を合計すれば良いです。
100000文字の文字列Tが与えられる。これの各prefixにおいて、相異なるsubstringで回文であるものの個数を求めよ。
+
...
各位置のsuffixについて、これ以上の長さのものは前に出てこないみたいな長さを列挙する必要があり、それにSuffix AutomatonとかSuffix Arrayやらが使えたりします。
50000文字の文字列Sと、10個のクエリP_iが与えられる。Sのあるsubstringで、
P_iでの出現回数がl_i回以上、r_i回以下であるのがすべてのiについて成り立つようなものの個数を求めよ。
250000文字の文字列A,Bが与えられるので、A,Bの最長共通substringの長さを求めよ。
A,BをつないでSA-IS+LCPでもいけますが、ローカルだとSuffix Automatonのほうが速かったです。でも実装によるのか。
250000頂点の文字木が与えられる。
50000個のクエリが与えられるので文字木のrootから葉に下るパスの相異なる文字列に対し、
クエリで与えられたアルファベット順でK番目のものを答えよ。存在しない場合は-1を返せ。
'a','b'からなる50000文字が与えられるので、substringのうち最大の繰り返し数を求めよ。
100000文字の文字列Sが与えられるので、Sのsubstringのうち、繰り返し数最大のもので、辞書順最小のものを求めよ。
同じsubstringを扱う問題でも、長さの連続性を扱う問題は苦手なんじゃないかなと思います。
200000文字の文字列S1,S2が与えられる。各iについて、S1[A,A+i)=S2[C,C+i)となる組(A,C)の個数をそれぞれ求めよ。
参考文献
http://e-maxx.ru/algo/suffix_automata
Finding Maximal Repetitions in a Word in Linear Time
A simple algorithm for computing the Lempel-Ziv factorization
-
最終更新:2014年05月22日 18:25