高度な2D描画について
グラフの演習では，学生がグラフ用紙になるべく正確なグラフを描くことにより，グラフの概形を理解できるようになります．図入り教材だけでなく，試験の解答用紙等にもグラフ用紙を自在に挿入できると便利です．そこで，グラフ用紙のプロットデータを生成するKETpicコマンドGraphpaperの定義を以下に紹介します．
function Out=Graphpaper(varargin);
if length(varargin)==1 then
Dx=varargin(1);
Dy=varargin(1);
else
Dx=varargin(1);
Dy=varargin(2);
end
GpL=list();
Nx1=floor(Xmax()/Dx);
for I=1:Nx1
GpL($+1)=Listplot([Dx*I,Ymin()],[Dx*I,Ymax()]);
end
Nx2=floor(-Xmin()/Dx);
for I=1:Nx2
GpL($+1)=Listplot([-Dx*I,Ymin()],[-Dx*I,Ymax()]);
end
Ny1=floor(Ymax()/Dy);
for I=1:Ny1
GpL($+1)=Listplot([Xmin(),Dy*I],[Xmax(),Dy*I]);
end
Ny1=floor(-Ymin()/Dy);
for I=1:Ny1
GpL($+1)=Listplot([Xmin(),-Dy*I],[Xmax(),-Dy*I]);
end
Out=GpL;
endfunction
以上のプログラムをScinotesにコピーして実行すると，下図のグラフ用紙が生成されます．
Setwindow([-3,5],[-5,5]);
Gp=Graphpaper(0.8,0.9);
Windisp(Gp,"c")
領域を指定する場合に，KETpicコマンドHatchdataを用いて斜線塗りで表示します．例えば，2曲線
,
で囲まれる部分のうち，
の範囲だけを指定する場合について考えてみましょう．
Setwindow([-1,7],[-2,2]);
G1=Plotdata("sin(x)","x=[0,2*%pi]");
G2=Plotdata("cos(x)","x=[0,2*%pi]");
H1=Hatchdata("ii",list(G1,"n"),list(G2,"s"));
Windisp(G1,G2,H1,"c");
hatchdata1.gif
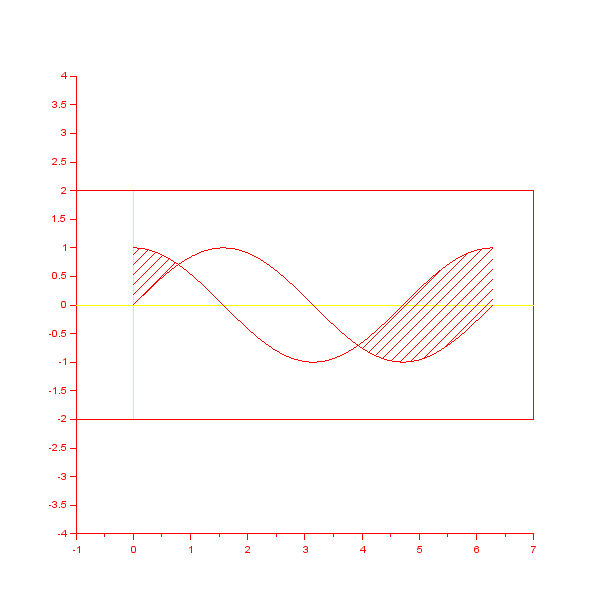
このように，Hatchdata内で領域を指定する方法には限界があり，すべての場合を実現できる訳ではありません．そこで，領域を確実に指定するためのKETpicコマンドEnclosingがあります．指定したい領域は左側の斜線部分だけだから，2曲線とy軸で囲まれた領域です．プログラムは以下のようになります．
Setwindow([-1,7],[-2,2]);
G1=Plotdata("sin(x)","x=[0,2*%pi]");
G2=Plotdata("cos(x)","x=[0,2*%pi]");
Yax=Listplot([0,Ymin()],[0,Ymax()]);
E1=Enclosing(list(G1,Invert(G2),Invert(Yax)),[0,0]);
H1=Hatchdata("i",list(E1));
Windisp(G1,G2,H1,"c");
描画をする際に，曲線の一部を指定しなければならないことが多々あります．曲線の両端のx座標が既知の場合は簡単に指定できますが，未知の場合はそれらを計算させて求めなければならず，面倒な作業になります．例えば，円
と直線
で切り取られる弦を指定する場合には，2次方程式
の実数解を求める必要が生じます．しかし，2曲線の交点を求めるKETpicコマンドIntersectcrvsを用いれば，この2次方程式を計算することなく，弦を指定することが可能です．プログラムは以下の通りです．
Setwindow([-3,3],[-3,3]);
C1=Paramplot("[2*cos(t),2*sin(t)]","t=[0,2*%pi]");
L1=Plotdata("2*x+1","x");
IpL=Intersectcrvs(L1,C1);
Ip1=IpL(1);
Ip2=IpL(2);
PL1=Partcrv(Ip1,Ip2,L1);
Windisp(C1,PL1,"c")
直線上の等分点を指定するには，内分点の座標の公式
を用いれば簡単に得られます．では，曲線上の等分点を指定するにはどうしたらよいのでしょうか？数学的には，積分を用いて曲線の長さを求めなければならないが，KETpicで曲線のプロットデータを求めると，x座標について等分された曲線上の節点の座標が得られます．実際には，曲線のプロットデータはこれらの節点を折れ線で結んだものだから，KETpicコマンドPointoncrvを用いれば，
番目の節点から
だけ進んだ点の座標を数値
で指定できます．例えば，正三角形ABCの角Aのマークを表すKETpicコマンドAnglemarkの中点を指定して
と表示するには，以下のプログラムになります．
Setwindow([-1,4],[-1,4]);
A=[0,0];
B=[3,0];
C=[3*cos(%pi/3),3*sin(%pi/3)];
Tabc=Listplot([A,B,C,A]);
Ama=Anglemark(B,A,C);
Nama=Numptcrv(Ama);
Ma=Pointoncrv(Nama/2,Ama);
Windisp(Tabc,Ama,Ma,"c")
pointoncrv1.gif
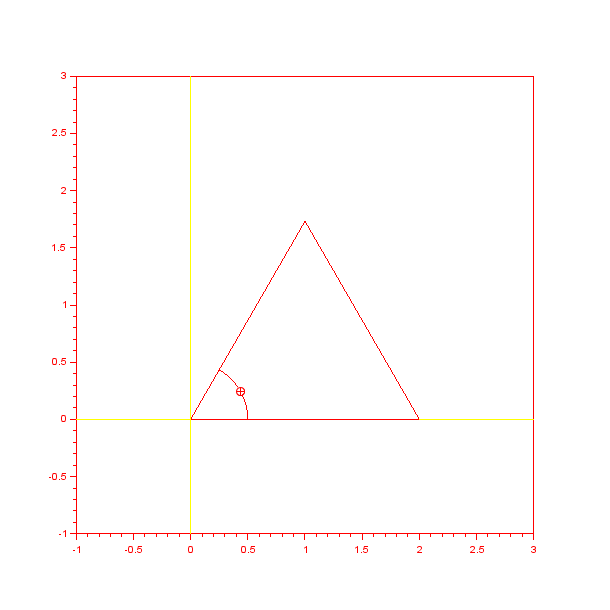
このプログラムでは，KETpicコマンドNumptcrvで角AのマークAmaの節点数Namaを求め，数値
でマークの中点Maを指定しています．
と表示するには，以下のプログラムで図ファイルpointoncrv_fig.texに書き出します．
Openfile("pointoncrv_fig.tex","1cm");
Drwline(Tabc,Ama);
Letter(A,"sw","A",B,"se","B",C,"n","C");
Expr(Ma,"ne","60^{\circ}");
Closefile("0");
偏微分や重積分では，2変数関数のグラフ（曲面）の描画が必要となります．KETpicコマンドSfbdparadataは2変数関数のグラフを稜線による線画で表示します．例えば，鞍点の例で頻出される2変数関数
のグラフを作成してみましょう．KETpicコマンドSetangleで空間上で投影する方向を指定し，Sfbdparadataでこの2変数関数のグラフの稜線を表示します．Skeletonparadataで投影した稜線を表示すれば曲面の描画ができ上がります．さらに，座標軸を追加しましょう．Xyzax3dataで座標軸のプロットデータを作成しますが，実際には，曲面の外側に現れる部分だけを取り出して表示することが必要になります．そこで，Crvsfparadataを利用します．また，曲面の後ろ側に隠れたプロットデータもCrvsfHiddenDataで取り出すことができます．これらは投影しても曲面の稜線と重ならないので，Projparaで投影すれば表示できます．以上のプログラムは以下のようになります．
Setangle(70,25);
Fd=list("z=x^2-y^2","x=[-2,2]","y=[-2,2]");
S1=Sfbdparadata(Fd);
Ax=Xyzax3data("x=[0,4]","y=[0,4]","z=[-2,5]");
Axo=Crvsfparadata(Ax,S1,Fd);
Axh=CrvsfHiddenData();
Setwindow([-5,5],[-5,5]);
Ps1=Skeletonparadata(S1,Axo,2);
Paxo=Projpara(Axo);
Paxh=Projpara(Axh);
O=Parapt([0,0,0]);
Windisp(Ps1,Paxo,"c")
surface1.gif
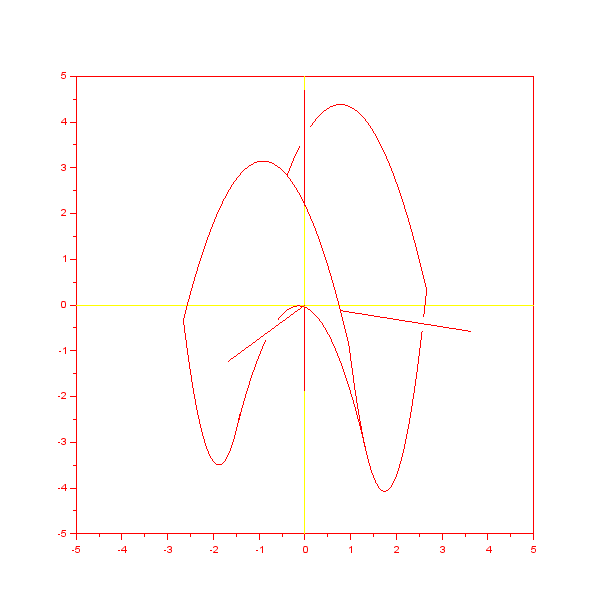
あとは，図ファイルsurface_fig.texに書き出すだけです．曲面に隠れた座標軸部分Paxhは点線で書き出します．Xyzaxparanameは座標軸の名前だけしか表示しませんので，Letterで原点名も表示させます．書き出しのプログラムを以下に記します．
Openfile("surface_fig.tex","1cm");
Drwline(Ps1,Paxo);
Dottedline(Paxh);
Xyzaxparaname(Ax);
Letter(O,"nw","O");
Closefile("0");
surface2.gif
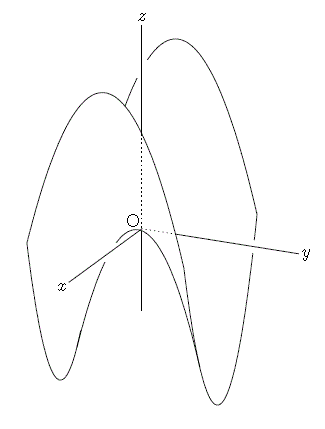上級者のページトップへ戻る．
作表については，TeXの作表環境tabularまたはarrayがありますが，これらで作表すると各セルの幅は挿入する文字列や数式の長さに従って自動計算されてしまい，等間隔のセル幅を実現できません．具体的に，1変数関数の微分法の応用として，曲線
の概形を求める問題で増減表をarray環境で作成してみましょう．
ここで，増減表の曲がった矢印を表示するために，スタイルファイルmathtipis.styを使いましょう．このスタイルファイルは
http://mixedmoss.com/mathtips/Japanese/mathtips.sty
を右クリックして、拡張子がstyであることを確認し，TeX文書と同じフォルダに保存します．あとは，TeX文書ファイルのプリアンブル部に
\usepackage{mathtips}
を書き加えればOKです．TeX文書をコンパイルすると，以下の表が出力されます．
tabledata0.gif
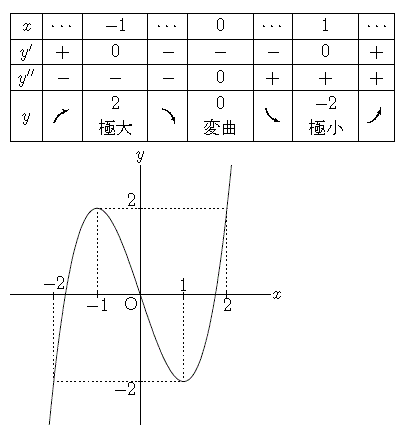
array環境で等間隔のセル幅を実現するには，文字幅を正確に計算しなければならず，困難を極めます．そこで，KETpicでは指定したセルの幅で作表できるコマンドTabledataを導入しました．当然，各セルには文字列や数式だけなく，図表も挿入することができます．Scilabだけでも作成できるのですが，現在の作表機能はKETCindyが最も進んでいるので，本節ではKETCindyによる作表で紹介します．まず，Cinderellaを立ち上げ，tabledata.cdyを作成します．CindyScriptに以下のようなプログラムを記しましょう．
Ketinit();
tate=[10,10,10,10,10,10,10,10];
yoko=[15,15,15,15,70];
rmvyoko=["r5c0c1"];
rmvtate=["c0r4r5","c2r4r5","c3r4r5","c4r4r5","c5r4r5","c6r4r5","c7r4r5"];
rmv=concat[rmvyoko,rmvtate];
Tabledata("",tate,yoko,rmv);
Changetablestyle(["r0c0c8","c8r0r5","r5c1c8","c1r0r5","r4c0c8","c0r0r4"],["dr,2"]);
Putrowexpr(1,"c",["x","\cdots","-1","\cdots","0","\cdots","1","\cdots"]);
Putrowexpr(2,"c",["y`","+","0","-","-","-","0","+"]);
Putrowexpr(3,"c",["y``","-","-","-","0","+","+","+"]);
Putrow(4,"c",["$y$","$\uzarrow$","\begin{tabular}{c}$2$\\ 極大\end{tabular}","$\ugarrow$",
"\begin{tabular}{c}$0$\\ 変曲\end{tabular}","$\sgarrow$",
"\begin{tabular}{c}$-2$\\ 極小\end{tabular}","$\szarrow$"]);
Putcell("c1r4","c8r5","c","\input{tabledata-fig.tex}");
Windispg();
※Putrow(4,...);の部分は長いので，読みやすくするために改行して半角空白文字を行頭に入れてあります．コピーして利用する場合には，改行と半角空白文字を削除してください．
上記プログラムで，rmvは削除する罫線のリストを指定しています．例えば，4行目のrmvyokoで，横罫線"r5coc1"は，横罫線R5のうちで縦罫線C0との交差点から縦罫線C1との交差点までの部分を指定しています．また，Changetablestyleは罫線の種類を変更できます．オプション引数["dr,2"]で2倍の太さの実践を指定しています．さらに，PutrowexprやPutrowで各行に文字や数値を代入し，Putcellで指定された範囲のセルに図ファイルtabledata-fig.texを挿入しています．
上記プログラムを実行すると，Cinderellaのメイン画面は以下のように表示されます．
tabledata1.png
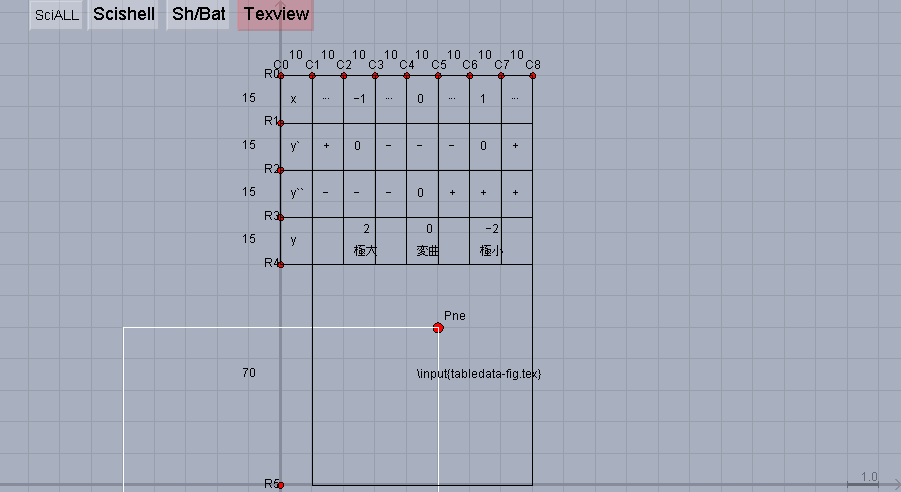
このままTexviewボタンを押して，Windowsならば，batファイル（Macintoshならばshファイル）を実行しても，スタイルファイルmathtips.styを読み込むことができません．そこで，Windows版ライブラリファイルketcindylib.txtを改良して，自分用のライブラリファイルmyketcindylib.txtを作成しましょう（Macintosh版ライブラリファイルketcndy.shでも同様です）．まず，ketcindylib.txtを別名で保存してmyketcindylib.txtを作成しておきます．myketcindylib.txtを開いて「Viewtex」を検索すると，
Viewtex():=(
regional(texfile,tmp,tmp1);
texfile=Fhead+"main";
SCEOUTPUT=openfile(texfile+".tex");
println(SCEOUTPUT,"\documentclass{article}");
println(SCEOUTPUT,"\usepackage{ketpic,ketlayer}");
println(SCEOUTPUT,"\usepackage{amsmath,amssymb}");
println(SCEOUTPUT,"\usepackage{graphicx,color}");
println(SCEOUTPUT,"");
println(SCEOUTPUT,"\def\ketcindy{{K\kern-.20em%");
...
と書かれています．この\usepacage{...}群の最後に\usepackage{mathtips}を追加します．
Viewtex():=(
regional(texfile,tmp,tmp1);
texfile=Fhead+"main";
SCEOUTPUT=openfile(texfile+".tex");
println(SCEOUTPUT,"\documentclass{article}");
println(SCEOUTPUT,"\usepackage{ketpic,ketlayer}");
println(SCEOUTPUT,"\usepackage{amsmath,amssymb}");
println(SCEOUTPUT,"\usepackage{graphicx,color}");
println(SCEOUTPUT,"\usepackage{mathtips}");
println(SCEOUTPUT,"");
println(SCEOUTPUT,"\def\ketcindy{{K\kern-.20em%");
...
LaTeXのスタイルファイルが作成できると，自分用のLaTeXコマンドが利用できます．スタイルファイル作りは「LaTeXマクロ」作りといわれ，高度なLaTeXプログラミングの知識を必要とします．しかし，KETpicを用いれば，初歩的なプログラミングの知識だけで高度なLaTeXプログラムを作成でき，「LaTeXマクロ」も簡単に作れます．前章では，増減表の曲がった矢印を表示するために，既存のスタイルファイルmathtipis.styを使用しました．本章では，このスタイルファイルの代わりに自分用のスタイルファイルbentarrow.styを作成し，関数
の増減表を作成しましょう．まず，4種類の曲がった矢印の図を作成します．
Setwindow([0-0.1,1+0.1],[0-0.1,1+0.1]);
Cnet=Paramplot("[1,0]+[cos(-t),sin(-t)]","t=[%pi,%pi+%pi/2]");
Cneb=Paramplot("[0,1]+[cos(t),sin(t)]","t=[-%pi/2,-%pi/2+%pi/2]");
Cset=Paramplot("[0,0]+[cos(-t),sin(-t)]","t=[3/2*%pi,3/2*%pi+%pi/2]");
Cseb=Paramplot("[1,1]+[cos(t),sin(t)]","t=[%pi,%pi+%pi/2]");
Windisp(Cnet,Cneb,Cset,Cseb,"c")
これをスタイルファイルbentarrow.styに4個のLaTeXコマンド\netarrow，\nebarrow，\setarrow，\sebarrowとして書き出します．LaTeXコマンドの定義には\newcommandを使用し，LaTeXコマンドを直接書き出すのにはKETpicのTexcomを使用します．これらの書き出しのプログラムは以下の通りです．
Openfile("bentarrow.sty");
Texcom("\newcommand{\netarrow}{");
Beginpicture("0.8cm");
Drwline(Cnet);
Arrowhead([1,1],Cnet,1,18,"ta");
Endpicture(0);
Texend();
Texcom("\newcommand{\nebarrow}{");
Beginpicture("0.8cm");
Drwline(Cneb);
Arrowhead([1,1],Cneb,1,18,"ta");
Endpicture(0);
Texend();
Texcom("\newcommand{\setarrow}{");
Beginpicture("0.8cm");
Drwline(Cset);
Arrowhead([1,0],Cset,1,18,"ta");
Endpicture(0);
Texend();
Texcom("\newcommand{\sebarrow}{");
Beginpicture("0.8cm");
Drwline(Cseb);
Arrowhead([1,0],Cseb,1,18,"ta");
Endpicture(0);
Texend();
Closefile();
ここで，通常，図ファイルの作成に使用されるKETpicコマンド
Openfile("bentarrow.sty","0.8cm");
...
Closefile("0");
を使用していないことに注意してください．曲がった矢印の図は
Texcom("\newcommand{\netarrow}{");
...
Texend();
内で作成する必要があります．そこで，ファイルを開くだけで，picture環境を書き出さないKETpicコマンド
Openfile("bentarrow.sty");
...
Closefile();
を使用し，picture環境をKETpicコマンド
Beginpicture("0.8cm");
...
Endpicture(0);
で書き出します．作成されたbentarrow.styを開いて，このような形で書き出されていることを確認してみてください．
bentarrow.sty
最後に，KETCindyを用いて増減表を作成し，前章で述べたように，自分用のライブラリファイルmyketcindylib.txtのViewtexコマンドの定義内に
println(SCEOUTPUT,"\usepackage{bentarrow}");
最終更新：2015年02月23日 13:14
