FFT - @zigen 's note

FFT（高速フーリエ変換）の使い方

今回使用するFFTライブラリ

y(t) -> Y(ω) : 時間の関数yを周波数空間へ

y(x) -> Y(k)：位置の関数yを波数空間へ

Tω=2π, Xk=2πより周波領域、波数領域への変換を簡単に行う。

京都大学の大浦 拓哉先生のFFT

http://www.kurims.kyoto-u.ac.jp/~ooura/fftman/

今回は上記のFFTライブラリの使い方をC言語、Fortranで説明します。

Fortran

データの作成

!=======================================================================
!                   FFT Test code
!    ----- fast fourier transfer test code -----
!    coder : Daisuke Saito
!    date  : April 11, 2010
!
!         (1)set the initial data about N, pi
!         (2)set the initial data for f(i)
!         (3)f(i) transfer datas in a(i)
!         (4)FFT for a(i)
!         (5)out put 
!=======================================================================
   program main
   integer nmax, nmaxsqrt, i 
   parameter (nmax = 32768, nmaxsqrt = 128)
   integer N, ip(0 : nmaxsqrt + 1)
   real*8 :: a(0 : nmax), f(0 : nmax), w(0 : nmax*5/4 - 1), pi, dx
   open(100, file="sin.txt")
   open(101, file="spectram.txt")
   write(100,*) "#i, argument, amplitude"
   write(101,*) "#i,  powerspectram"
   N = nmaxsqrt
   pi = dacos(-1.d0)
   dx = 1.d0/N
   ip(0) = 0
   a(:) = 0.d0
   do i = 0, N
       f(i) = dsin(2.d0*pi*i*dx) + dsin(30.d0*2.d0*pi*i*dx) + 3*dsin(7.d0*2.d0*pi*i*dx) !<-この行で初期振動をセット
       write(100,*) i, 2.d0*pi*i*dx, f(i)
   enddo
   do i = 0, N
      a(2*i) = f(i) !<-Point1
   enddo
!---Kyoto-u FFT subrotine--
   call cdft(2*N, 1, a, ip, w) !<- Point2
   do i = 0, N/2 - 1
       write(101,*) i, 2.d0*dsqrt(a(2*i)*a(2*i)+a(2*i+1)*a(2*i+1))/N !<-Point3
   enddo
   close(100)
   close(101)
   end program main

Point1

今回複素フーリエ変換するのため実数と複素数の入れ物を用意しなければならない、そこでaという入れ物を用意しアーギュメントiが偶数にフーリエ変換したい関数の実数部、iが奇数に虚数部をセットする。

注：今回は虚数部の値がないので、実数部だけ。

Point2

拓哉先生のFFTの説明どおり、cdft(2*N, 1, a, ip, w)を設定

Input: 2*N = 複素FFTをかける配列の大きさ、今回は実部がN個、虚部がN個なので2N個

Input: 1は普通のFFT、-1は逆変換

Input&Output:　変換するデータ、出力データは同じ配列に上書きされる

Input:　？

Output:　ワーキング領域

Point3

今回パワースペクトルP(k)を出力したいのでP(k) =|F(k)|^2/N= Fre(k)*Fim(k)/Nを出力

Inputデータ

今回入力するデータは f = sin(x) + sin(30x) + 3sin(7x)

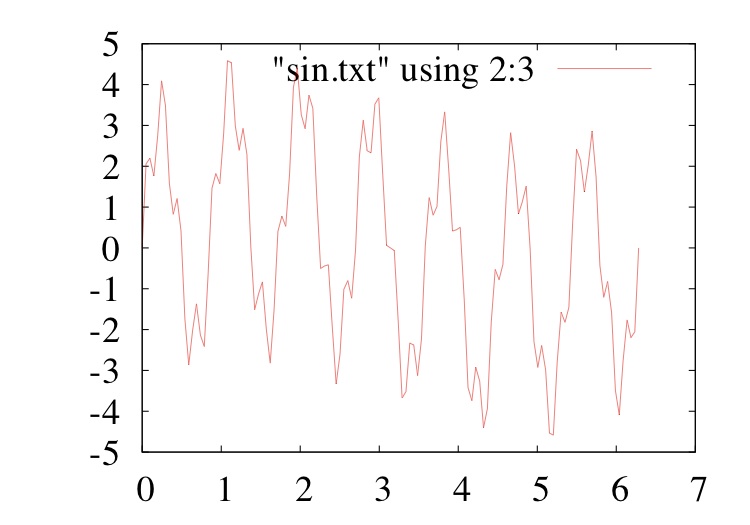
Outputデータ

パワースペクトルのピークがk=1,7,30のところに出ている。

今回使用したデータとか全部

https://docs.google.com/leaf?id=0B08q5BonMYJVMGEzNDkzZGMtOThkMC00OWRkLTk5NzctODVmOTQ2NWUyYmM1&hl=ja

C言語

データの作成