まずは確認しておきたい常識的事項
まずは当たり前のことを確認しておきます。
- 誤解されやすい常識1)一般社会には、「かけ算の式の順序に関するルール」はありません
常識1の正確な記述)一般社会には、常に「一つ分×幾つ分」または「一つ分×幾つ分」の順序で書かなければならないという「かけ算の式の順序に関するルール」はありませんけど、 常識的なルールとして 「一つの様式において「一つ分×幾つ分」または「一つ分×幾つ分」のどちらかの順序を採用したら、その様式ではそれを守る」というもの があります
- まちがった常識2)科学的にも、つまり数学の世界においても、そのようなルールはありません
常識2の正しい記述)科学の世界においても「一つの様式において「一つ分×幾つ分」または「一つ分×幾つ分」のどちらかの順序を採用したら、その様式ではそれを守る」というルールはもちろんあります。さらに、数学の世界では「より厳密な扱い」をします。また慣用的な「かけ算の式の順序に関するルール」があります。たとえばスカラーは左からかけるのが慣用です。この慣用的なルールを破って右からかける書き方をしてもまちがいではありませんが、「特別な合理的理由があってそうする場合を除いて」慣用的ルールに従わないことは意思疎通を徒に困難にするだけです。ですから、数学を含む科学の世界において「一つの様式において「一つ分×幾つ分」または「一つ分×幾つ分」のどちらかの順序を採用したら、その様式ではそれを守る」というルールはもちろんある上に、慣用的な書き方のルールも存在します。ただその「慣用的な書き方のルール」が絶対的なものではないというだけのことです。
- 常識3の不正確な記述)したがって、小学校の教育は「卒業時にはかけ算の順序はどちらでもいいと知っている」ように教えるべき。(それをせずに常識1,2に反するルールを教えたままにしておくのは教師として無責任?)
常識3の正しい記述)そもそも常識1や常識2について正しく知らない人が「小学校の教育は「卒業時にはかけ算の順序はどちらでもいいと知っている」ように教えるべき。」などと断言してはいけません。現在の算数では小学校2年生に対して3個のおまんじゅうののったお皿が5皿あるときのおまんじゅうの総数を3×5とあらわすと教えています。3個のおまんじゅうののったお皿が5皿あるときのおまんじゅうの総数も5個のおまんじゅうののったお皿が3皿あるときのおまんじゅうの総数も同じですから3×5=5×3となります。ですから「3個のおまんじゅうが5皿あるときのおまんじゅうの総数は3×5でも5×3でもあらわされる(計算できる)」というのは正しい言い方です。ですが、この事実(交換法則)を理解するためにはどうしても3×5と5×3を区別しなければなりません。はじめから3個のおまんじゅうが5皿あるときのおまんじゅうの総数は3×5でも5×3でもあらわされるといってしまうのはトンデモ的な理解(または循環論法)です。循環論法でこどもたちを煙にまくような教え方をすることをトンデモ教育といいます。少なくとも現在の算数の教科書の記述は理にかなっているものです。一部の先生方が「掛け算の順序の指導」を徹底していることがよくネットで批判的に取り扱われますが、いま書いた理屈を踏まえた批判ではないこと(つまりトンデモ批判)が多いです。なお一般人が「教師として無責任」などという批判をするのは行き過ぎです。
- 正しい常識4)小学校の教育は「卒業時には、累加としての掛け算(一つ分×幾つ分も同様)は表記法が固定されるが、交換法則が成り立つと知っている」ように教えるべき。(それをせずに常識2のように教えてしまうのは教師として失格。また常識2や3のようなまちがった常識をもとに「教師として無責任」などと断ずるのは一般人の越権行為。やってはいけません。)
正しい常識4)小学校の教育は「卒業時には、累加としての掛け算(一つ分×幾つ分も同様)は表記法が固定されるが、交換法則が成り立つと知っている」ように教えるべしというのは正しいです。それが教えるべきすべてです。注意したいのは「3×5も5×3もどちらでも(意味も含めて)まったく同じ」などというトンデモ標語として教えないようにすることです。正しい理解をせずに標語的な理解しか持っていないために大人になっても「3×5も5×3もどってでも同じ」という理解を超えることができない人たちがたくさんいるようです。そういう基本的な理解があやふやでも「正しく計算することさえできれば」ペーパーテストではよい成績をとれるため、高学歴の人たちにもそういうまちがった理解をしている人が多いです。「教師として無責任」などと断ずるのはそういう人たちに多いようです。
以上の4点について「言うまでもなく、それは当然のことだ」と思える方は、
(OKwaveでの質問「子供5人にお菓子2個ずつ」のコメントに「小学校の間はこの立式で通します」と明言する「小学校校長(自称)」tosa-bash氏登場)
(バカにした内容ではない。偏見と中傷もほどほどに。)
といった事例に唖然とされることでしょう。
とはいえ、上の4点を踏まえた上でこの事例に唖然とされるようなら、このページのこの先は読まなくて大丈夫です。
逆に、常識1~4にちょっとでも疑問や不安を感じる方は、この先も読んでください。
常識1)一般社会には「かけ算の式の順序に関するルール」はありません
たとえば請求書を書く場合、
数量 × 単価 = 金額
単価 × 数量 = 金額
と、どちらの書式で書かれている請求書も普通に存在します。
どちらで書くかは会社の都合に応じて決めればいいだけの話で、どちらが金額でどちらが個数か誤解が起きないようになってさえいれば問題はありません。ですから 一枚の請求書内の一つの欄で2つの書式が混在しているのは好ましくありません。 そういう意味では「かけ算の式の順序に関するルール」はあることにも注意して下さい。
そういう書き方は、単価がころころ変わるものによく使うような気がします。
切手のように、誰が何枚買っても値段が変わらないものならば確かに50x750でしょう。
でもパンフレットというのは「50円のもの」ではありません。
「1部を作るのに50円かかったもの」なのです。
もしかしたら1000部を超えた分は35円で作れるかもしれません。
その場合(例:1200部)は
1000x50=50000(1000部は単価50円)
200 x35=7000 (200部は単価35円)
と書くのです
という人がいますがこんなルールはありません。
50x1000=50000(1000部は単価50円)
35 x200=7000 (200部は単価35円)
と書いてもいいのです。ですが
50x1000=50000(1000部は単価50円)
200 x35=7000 (200部は単価35円)
と書くのはよくない、というのは一般社会でもルールです。ルールがあります!
「50円のものを1000部と35円のものを200部買った」
という考え方が当てはまらないのがお分かりになりますね?と言われて 「分かる」はずがない ですよね。
なぜなら、こんな考え方のルールはないのです。繰り返しておきますが
「値段が違う2種類の品ではなくて単価が違うので、このように書きます。 」というルールはありません。
常識2)科学的にも「かけ算の式の順序に関するルール」はありませんと思っている人が多いようですがそれはまちがいです。
行列の積なら A×B≠B×A ですが、小学生にかけ算には行列は何の関係もありません。
逆に、実数の範囲で数式を使った計算を自由にこなせるようにするためには、交換法則
A×B=B×A
のほうをしっかり教え込んでおく必要があります。そう思うのは正しいのですが
交換法則があるから数学では掛け算の順序を考えない
というのは大多数の勉強不足の素人の浅知恵です。詳しくは黒木玄さんの論考を見て下さい。
常識3)小学校卒業時には「かけ算の順序はどちらでもいいと知っている」ように教えるべき
これをせずに常識1,2に反するルールを教えたままにしておくのは教師として無責任なこと、と宣う人がおりますが
何様のつもりでしょう。もちろん常識1,2に反したことを教えるようなよく分かっていない教師は教師として失格です。
ですが高等数学はもちろん中学数学さらには算数さえ根本的に理解している一般人がどのくらいいるのでしょうか。
(何を書くべきか考え中)
この指導で何の問題もなし。シロートの無責任な口出し無用である。と言われたら反発したくもなります。
ですが、プロの仕事に素人が分からぬ口をはさめば、そう言われても仕方ないかもしれません。
「たかが掛け算」と思って口をはさんでいるのでしょうが、もっと謙虚になりましょう。
たとえば論考で(→
黒木玄さんの論考目次)書いていることが当たり前のようにお分かりになりますか。
常識4)常識2や3のようなまちがった常識をもとに「教師として無責任」などと断ずるのは一般人の越権行為。
厳として戒めるべし。
▶「かけ算とは1あたりから全部の数を求める計算であるとし(それを)1あたり×いくら分 の順序でかくとき,1皿あたり8個の2皿分の総数を8×2個とかく」
(という当たり前の論理に従った考え方)から
「1あたり×いくら分 の順序でかく」だけをとりだして「きまり(掛け算順序の絶対的なルール)」(として教えている)と「批判」しても(その批判は)ナンセンスでしょう。
▶「かけ算の順序」などといった言葉はそうしたナンセンスな(批判)を誘発する。それだけをとりだして
「どっちだっていいだろ」というのはさらに(論理的にも)ナンセンスでしょう。いつの間にか
「かけ算とは1あたりからいくら分を求める計算であるとし,1あたり×いくら分 の順序でかくとき,1皿あたり8個の2皿分(の総数)を2×8個とかく」でもいいだろ
なんて(非論理的なメタメタな)ことになる。
▶実際然う考える一般大衆(その中には大学教員や研究所勤務など所謂知的職種の連中も居る)が増えているようだ。それは「掛け算順序批判派」の連中がことばをていねいに使わぬ批判のための批判に終始して居ることが大きな要因であろう。大騒ぎしている連中にはその反啓蒙的行為の責任がある。
常識5)掛け算順序を適当に書いてバツにされた答案に憤る前に知っておいて欲しいこと。
以下は順序をまちがえてバツにされた典型的な例です。
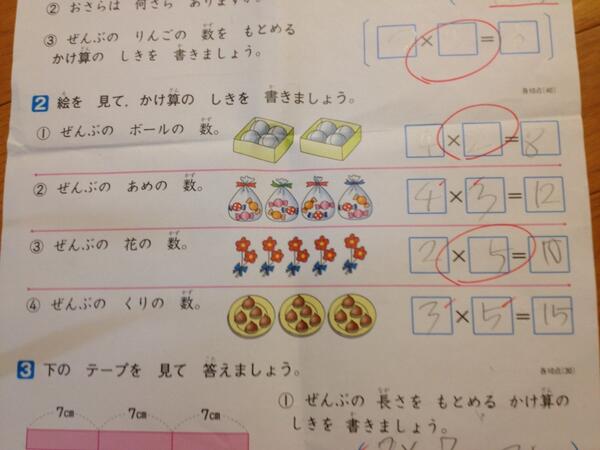
(これを貼った本人のツイート)ダメだこりゃ。
このひとは算数とは計算できればいいとでも思っているらしいですね。このツイートを引用して
ローカルルールかどうかは知りませんが、順序固定が非合理であることは間違いないと思います。
などと言っているひとたちも同じ。よく見て下さい。この答案。
問題2の小問1〜3と小問4で書き方に整合性がない(非合理)ですよね。つまりあまりわかってないんです。
2つの数をかければ答えになるということを覚えているだけ。小学校2年生にそれ以上の理解を求めるのは酷という意見はあると思いますけど、こういう答案がバツにされて「ダメだこりゃ。 」というのはおとなが分かっていないことを露呈していて、しかも正しい考え方を「ダメだ」と批判していることなので恥ずかしいことです。以下のようなツイートもされていました。
「3の厳密な単位は "個" じゃなくて "個/袋" 」って概念を教えないと、物理とかを学ぶ時につまづくことにならんか?と心配になる
この方は3の厳密な単位が「個」であってもよいことがわからないのです。ですから「3の厳密な単位は "個" じゃなくて "個/袋" 」と考えて3個という概念はないことにしたい(わからないから)ようですけど、これって「ものごとの正しい理由のわからない人」がよくやってしまうまちがい(過ち)ですよね。
ローカルルールかどうかは知りませんが、順序固定が非合理であることは間違いないと思います。
というツイートも。これもよくやってしまう過ちです。「非合理であることは間違いないと思います。」では「STAP細胞はあると思います。」と何も変わりません。「非合理であること」を提示できなければいけないのです。一方で、上のバツにされた答案ですが小問1〜4を通してみれば答案が「非合理であること」は一目瞭然ですよね。
※このページは編集できません。
最終更新:2014年07月21日 02:14
