初歩的モデルへの固執は成長を妨げる、が。。。 - 掛算順序固定問題対策本部（保管庫）

初歩的モデルへの固執は成長を妨げる

　さて、ここで算数の話です。
　「かけ算」を考えるとき、直観的に理解しやすいのは

「１あたり数　×　いくつ分」

　のモデルのほうである、という主張には別に違和感はありません。
　大きな数にそもそも馴染んでいない子供に対しては、「１あたり」を「いくつ」繰り返すことで数が増えていく、という事象に馴染んでもらい、それを簡単に書ける「かけ算」という表記法を教え、その練習をさせるというのは理にかなっています。

　ただ、いつまでもそれを引きずっていていいのか？　という話。

　「１あたり数　×　いくつ分」

　というのは「素朴な直観的モデル」のほうであり、「直観的で分かりやすいが応用範囲が狭い」わけです(メンタルモデルに関するページ参照)。それに対して、

　　　●　●　●　●
　　　●　●　●　●
　　　●　●　●　●

　こんな形に抽象化されたモデルは「直観的ではないが応用範囲が広く」なります。
　「応用範囲が広い」というのはたとえばこういう話です。

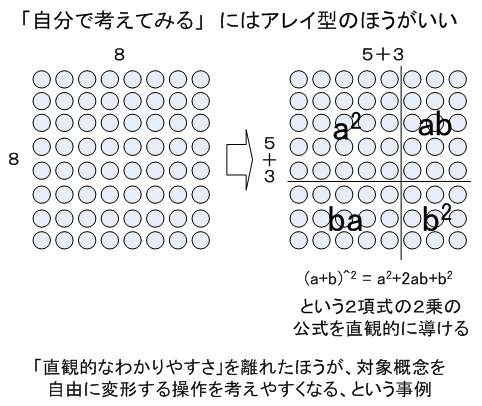
　「８×８」というかけ算を上図左側のようにアレイ化して考えれば、これを「５＋３」の2乗、と考えた時にそれが　（ａ＋ｂ）の2乗という2項式の2乗の展開公式が自然に導けますね。（中学生の内容ですが、中学生でもこのイメージを持たずに機械的に公式だけ覚えて試験をしのいでいる子は少なくないわけで・・・）

　こんなふうに、 「ここをちょっと変えてみるとどうなるんだろう？」「これをひとまとまりと考えるとどうなるんだろう？」と、ああでもないこうでもないと「数で遊んでみる」感覚は、算数であろうと数学であろうと非常に大事です。それがやりやすいのは上記のようなアレイ型のモデルを使った場合です。
「1あたり数×いくつ分」の立式をいくら強制してもこのような「数で遊ぶ」感覚は生まれてきません。

　つまり、

「1あたり数×いくつ分」モデルは直観的だが「数で遊ぶ」ことが不可能
アレイ型モデルは直観性に欠けるが「数で遊ぶ」おもちゃにしやすい

　どっちがいいの？　という話。
　こういうデメリットがあるにもかかわらず、単なるかけ算を認知させるための「１あたり数×いくつ分」という導入部のモデルにいつまでもこだわる理由がさっぱりわからないんですよね・・・
　なにも文字式や微積分をやってるわけじゃないんですから。

　また、メンタルモデルに関するページで既に書きましたが、「素朴で直観的なメンタルモデル」にいつまでも固執すると、つじつまが合わない部分に説明をつけるために、無理のあるロジックがいくつもいくつも出てくるものです。

２×８ならタコ２本足
単位でサンドイッチする形で式を書きましょう

　とか、この種の指導法は結局「１あたり数×いくつ分」というルールに固執する余りの苦し紛れの理屈にしか見えないわけです。