乗法計算機「1桁×2桁」 > 解説

乗法計算機「1桁×2桁」 特設解説ページ

	by tactics
	162票 ★★★★★
	2009/10/11 21:54
乗法計算機[1桁×2桁]	飛ぶ

ここは解説専用ページです。前文はこの記事をどうぞ

---

tacticsのパーフェクト長文覚悟回路教室

この回路は入力部、計算部、塩水加法演算部、表示部からなっており、
入力された信号を分解して複数の回路で計算し、集計をすることで省スペース化している。

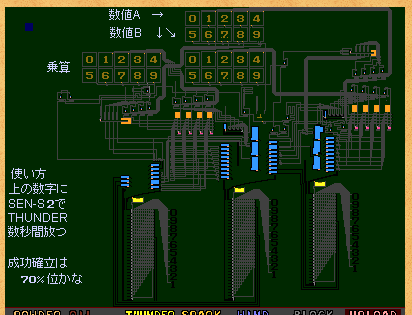
これからこのごり押しを極めた回路を解説していこうと思う

だが、その前に、4つの概念について軽く説明しよう

数の表記法	この計算機は5進数の束と2進数の導線によって計算している
計算の仕組	2種類の信号からどうやって1桁の掛け算をするか
全体の計算	1桁の掛け算から2桁×1桁の掛け算をする方法
加法計算機とタンク	最終的に必要な「塩水タンク」の数

METAL回路の基礎とこれが分ればこの「乗法計算機」はすぐにわかるようになるはず・・・

目次

---

この計算機の4つの概念と考察

数の表記法

この計算機では、1つの信号が2種類の導線の組み合わせによって扱われる。
それが「数を示す導線（4本束）」と「５を示す導線（1本）」だ、
1234 5
|||| |
「数を示す導線」は必ず4本のうちの1本しか電流が流れない。（流れたら回路の設計バグ）

例えば、いまここに「４という数を示す導線」が来て「５を示す導線」が来なかったとしよう
---4 -
---| -
すると、４＋０＝４となる。
次に、ここに「２という数を示す導線」と「５を示す導線」が来たとしよう
-2-- 5
-|-- |
そのときは、２＋５＝７という数を示すことになる。

数	"4本束"の示す数	"５"の導線	数	"4本束"の示す数	"５"の導線
0	0	OFF	5	0	ON
1	1	OFF	6	1	ON
2	2	OFF	7	2	ON
3	3	OFF	8	3	ON
4	4	OFF	9	4	ON

これ以降、4本束の導線を「数導線」、５を示す導線を「五導線」と言うことにする

入力回路

ここで、一旦入力された信号がどのように分別されるかを見てみよう

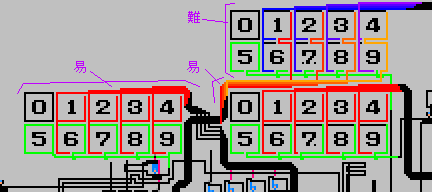緑：数導線、赤と紫：五導線

この図では2種類の入力装置がある。
上の一つが"難入力"で、下の二つが"易入力"である

種類	数導線	五導線
難入力	2束	1本
易入力	1束	1本

このうち、5以上のCLONEブロックは五導線を、
0と5以外のCLONEブロックはいくつかの数導線を出力している。（水銀がないために増幅が出来ない）

---

計算の仕組

ここで、数の表記法が判ったので、これでどうやって1桁と2桁の掛け算をするのかを説明しよう

まず、1桁同士の掛け算についてである。

たとえば、今ここに
---4 -
---| -
と
-2-- 5
-|-- |
という信号が来た場合、結果はどうなる？
答えは、４×７＝２８だ。出力は塩水タンクから出力させることになる
しかし、この場合は

（４＋０）×（２＋５）＝４×２＋４×５＋０×２＋０×５＝８＋２０＋０＋０＝２８

という計算をした方がいい。
何故なら、「掛け算九九」を3つの「ON/OFF演算」と一つの「掛け算五五」で表すことができるからであり、
塩水タンクを大きく節約出来るからである

ここで、掛け算九九をANT回路で表すとどうなるかを考えよう。

画像を表示

デカい。詰めるだけ詰めているがそれにしてもデカい。
しかもこれを2回するとなんだかんだでDot数が足りない気がしてくる

次に、「掛け算五五」を使うとこうなる。

画像を表示

ややましな程度といったところか？
だが、実際には装置の上に導線を這わせる必要がある訳でこれのほうが使いやすい。

といった感じにして一桁を計算するわけだ。

それぞれの演算回路の戻り値一覧
(1,2,3,4)×(1,2,3,4)	(0,5)×(1,2,3,4)		1~16	0 or 5~20
(1,2,3,4)×(0,5)	(0,5)×(0,5)		0 or 5~20	0 or 25

---

全体の計算

つぎに、一桁同士の掛け算からどうやって2桁と1桁の掛け算にするかだ。

次の例を見てみよう。

４８×７＝？

あなたならどう計算するでしょうか？
恐らく多くの人は紙と鉛筆を持ってきてこうするしかないだろう

　　４８
×　　７
────
　　５６
　２８
────
　３３６

それは、「掛け算九九」を知っているが「掛け算99×99」を知らないからだ
でも、掛け算九九と「足し算」を使うだけで掛け算が成立している。

では、こうするとどうだろうか

　　ＡＢ
×　　Ｃ　Ｂ×Ｃ＝ＤＥ
────
　　ＤＥ　Ａ×Ｃ＝ＦＧ
　ＦＧ　
────　ＤＥ＋ＦＧ×10＝ＨＩＪ
　ＨＩＪ

これで最初は「掛け算99×99」1つだったものが、
「掛け算九九」2つと「足し算」に変わった。

「掛け算九九」は前述の通り「掛け算五五と条件判断と足し算」により可能だ
更に足し算は大きな加算装置を利用することで省略ができる。

これで、作るべき演算回路は、

「掛け算五五」のANT分岐	1個×2組
五導線が来ると数導線の5倍の値を返す塩水分岐	2個×2組
2つの五導線が来ると25を返す塩水分岐	1個×2組
全てを足すのに必要な塩水加法計算機	3基

となった。

---

加法計算機とタンク

最後に、加法計算機はどのくらいの容量がいいだろうか。
さっき上で書いておいた表をもう一回見てみよう。

それぞれの演算回路の戻り値一覧
(1,2,3,4)×(1,2,3,4)	(0,5)×(1,2,3,4)		1~16	0 or 5~20
(1,2,3,4)×(0,5)	(0,5)×(0,5)		0 or 5~20	0 or 25

これは、数導線と五導線の演算でどのような値が返るかを示している。これを組み替えてみよう

タイプ名	演算の種類	返る値
数数乗算	数導線×数導線	1,2,3,4,6,8,9,12,16
数五乗算	数導線×五導線	0,5,10,15,20
数五乗算	五導線×数導線	0,5,10,15,20
五五乗算	五導線×五導線	0,25

これから、次のように考えられる

	塩水タンクの設置方式
タイプ名	10の位	1の位
数数乗算	1個のタンク	9個のタンク
数五乗算	2個のタンク	5のタンクを1個
数五乗算	2個のタンク	5のタンクを1個
五五乗算	2のタンクを1個	5のタンクを1個

これが、1つの「1桁同士の掛け算」に必要なタンクの数である。

実際にはこれが2つ並んでいる。しかも10の位になっている。よって、

		塩水タンクの設置方式
対象	タイプ名	100の位	10の位	1の位
1桁目×1桁	数数乗算		1個のタンク	9個のタンク
	数五乗算		2個のタンク	5のタンクを1個
	数五乗算		2個のタンク	5のタンクを1個
	五五乗算		2のタンクを1個	5のタンクを1個
2桁目×1桁	数数乗算	1個のタンク	9個のタンク
	数五乗算	2個のタンク	5のタンクを1個
	数五乗算	2個のタンク	5のタンクを1個
	五五乗算	2のタンクを1個	5のタンクを1個
合計	タンク	5個のタンク 2のタンク	14個のタンク 2のタンク 3個の5のタンク	9個のタンク 3個の5のタンク
取りうる値	数値	5+2=7	14+2+15=31	9+15=24
繰り上がり	タンク	なし	3つのタンク	2つのタンク
最終的なタンクの数	タンク	8個のタンク 2のタンク	16個のタンク 2のタンク 3個の5のタンク	9個のタンク 3個の5のタンク

となる。本当にそーなのかー？

感動のために敢えて色分けしない画像を用意しておいたので、
そこは画像で自分の目で確認してくれ

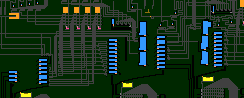
でも、わからん。という人は、↑の画像のタンクを色分けした画像を見てほしい

画像を表示 ネタバレ注意

数数乗算	紅
数五乗算	桜
五五乗算	橙
繰り上り	蒼

---

計算機を≪見る≫

最後に、全ての≪入力≫、≪乗算≫、≪加算≫について解説が終了したので、
色分けによってアノ回路を見て}いこう。

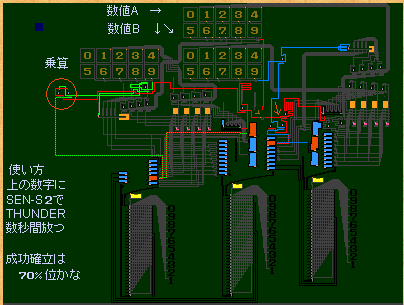
五導線に色を塗ってみるとこうなる。
また、五五乗算によって解放される塩水タンクを橙に塗ってみた。

五導線を水色で塗りつぶし、数導線に色を塗ってみた
解説がめんどくさくなってきたので、適当に目で追ってみれ～

おしまい

---

使われている回路一覧

★は乗算に直接かかわる回路

	入力装置	10ボタンの（難入力1つ、易入力2つ）
	塩水加法計算機(3繰り上がりまで対応)	3桁分の内中央は32、2つは29
	塩水タンク(1と2と5をあらわすタンク)	計算機に入れる
★	4,4-横主回路切断式ANT分岐	数数乗算（掛け算五五）
★	4-縦主回路接続式ANT分岐	数五乗算
★	ABどちらかから一瞬でも流れてくれば電気を流す回路	五五乗算
★	電流を流し続けると初めの一瞬だけ他方へ流す回路	五五乗算への入力を2回使うため（解説不能）
	単塩水分岐	判定のみでおよそ10Dot分しか使わなくてすむ
★	4-複塩水分岐	電流を流し(ryの次に数語乗算をさせるため（解説不能）

---

終わりに

普通に9*9のANT分岐でやろうとすると、横の長さは

n(7+n)+2　⇒　9(7+9)+2 = 9*16+2 = 146

となり、実にマップの横半分の長さを1つの回路で埋めることになってしまう
しかもそれだけでは動作しない(縦は3n+15=42でそれなりにある)
更にこの方法で出力されるのは幅100の端子から1つのみで、掛け算には向かない
1桁分でANT分岐を2つ作ればいいけどDotがあああああ

計算上は因数分解して別にかけたものを足し合わせる方が効率がいい
たとえば60*60をするとき、一括よりも(2,2,3,5)*(2,2,3,5)の方が効率はいい
ただし回路がテラとてつもない回路になる

（つまり、表にすると・・・）

	(0,1)	(0,1)	(0,1,2)	(0,1,2,3,4)
(0,1)	0,1	0,1	0,1,2	0,1,2,3,4
(0,1)	0,1	0,1	0,1,2	0,1,2,3,4
(0,1,2)	0,1,2	0,1,2	0,1,2,4	0,1,2,3,4,6,8
(0,1,2,3,4)	0,1,2,3,4	0,1,2,3,4	0,1,2,3,4,6,8	0,1,2,3,4,6,8,9,12,16

（で、分岐回路だけですごい数になって回路全体が更にカオス）

これで30000Dotだから2桁*2桁を作るにはもっと省スペース化するべきである
（まあ単純に考えて2倍以上ですから）

でも、今は水銀などの登場によってもっといい装置が作れるはずなので、実現は十分なのだ☆

夜景がきれい7×77を計算すると539になるっぽいです。