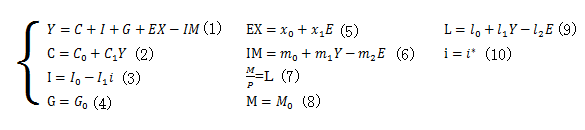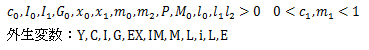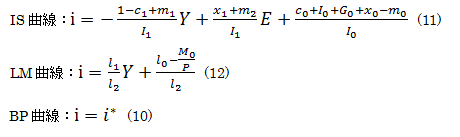マンデルフレミングモデル - 経済学メモ

IS-LM-BPモデルにおいて、「資本移動が完全に自由」「為替レートの静学的期待」という仮定をおき、
BP曲線を単純化したものがマンデルフレミングモデルである。
ここでは、このモデルの概要、財政政策と金融政策の効果について扱う。

• 「国際間の資本移動が完全に自由」とは
• 「為替レートの静学的期待」とは
• モデルの方程式体系

---

「国際間の資本移動が完全に自由」とは

このモデルは、「国際間の資本移動が完全に自由」という前提がある。
「国際間の資本移動が完全に自由」とは、国境や関税などの国際間の資本の移動にかかるコストを無視するということである。
この仮定は一体どのような意味を持つのか。
これを考えるためには国際間のポートフォリオ選択を考えなければならない。
資産ポートフォリオとは、自らの資産をどのような形(現金、株式、債券etc)で持つか、ということである。
ここでは、資産を債券として持つとして考える。

Aさんは自分の資産を国債として持ちたいと考えている。
自国であるA国と外国であるB国のどちらの国債が選択肢として登場している。
さて、Aさんはどちらの国債で資産を持つべきだろうか。
国債は債券なので当然利子が付く。なので普通はより利子率の高い方の債券を持とうとするだろう。
というわけでここでA国国債の利子率をi、B国国債の利子率をi*とする。
例えばi>i*の場合A国国債がより利子の付く儲かる国債ということになる。
しかし、これだけではどちらの国債を購入すべきかは決定できない。

B国はAさんにとって外国である。
よって通貨が異なるため、B国国債を購入するには両替を行う必要がある。
そうなると問題となるのが為替レートだ。
今考えているのは変動レート制のモデルであるので、
償還時に為替レートが変動していれば再び両替して自国通貨にした時に利子率通りの額にならないことになる。
したがって、利子率だけでなく為替レートの変動も考慮しなければならない。

というわけで為替レートと利子率を考慮して、償還時に何倍になるかを計算してみる。
ちなみにどちらの国債も1年もの(1度だけ利子を受け取って償還される)とする。
A国国債を購入した場合:
1年後の償還時に、利子率i分だけ上乗せされて返ってくるので、
1年後には購入時の値段の倍になる。
B国国債を購入した場合:
まず為替レートを設定しておく。E:現在為替レート、E*:将来為替レートとする。
どちらもA国通貨建て()としておく。
まず、A国通貨をB国通貨に交換するため倍する。
その次にその資金で国債を買い、1年後に利子が付き償還されるため倍になる。
しかしこのままでは単位がB国通貨のままとなるため、A国通貨に戻すためE*倍し、となる。

このようにして求められた倍率の大小によってAさんの取るべき行動が決定される。
→ A国国債を購入する…①
→ 無差別…②
→ B国国債を購入する…③
無差別というのはどちらを購入しても同じという意味だ。
これは一種の均衡状態であり、この状態であれば新たな取引を行うインセンティブは存在しない。

投資家というのはもちろんAさんだけではない。
A国B国のどちらにもたくさん居る。
例えば①の場合は、A国国債の方がより利益が出るのでA国の人はもちろんB国の人も欲しがる。
B国の人が購入するにはA国通貨に両替する必要があるので、A国通貨の需要が増大する。
A国通貨の需要が増大するため、A国通貨はB国通貨より相対的に強いことになる。
したがってA国通貨高が起こり、Eが低下することになる。
Eが低下するとが大きくなり、利益の差が縮まる。
このような動きが資本移動が完全に自由であるため、②の無差別の状態まで続く。
③の場合も同様でA国通貨安が起きてが小さくなり、②の状態へ向かう。
なので、「国際間の資本移動が完全に自由」という仮定からはが導かれる。
また、のことを金利裁定式(平価式)と呼ぶ。

「為替レートの静学的期待」とは

為替レートの静学的期待とは、為替レートが将来的に変化しないであろうと人々が考える状態のこと。
数式として表すとE=E*のことである。

このことと、「国際間の資本移動が完全に自由」を合わせると、i=i*という結果が導かれる。
マンデルフレミングモデルでは、これがBP曲線となる。

モデルの方程式体系

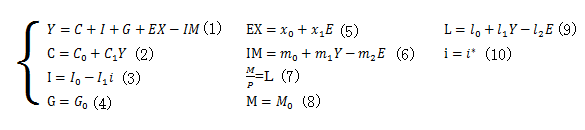
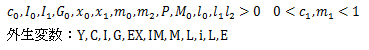
このモデルは以上の10本の式で構成される。
(1)、(2)、(3)、(4)、(5)、(6)をiについて解いたものがIS曲線、
(7)、(8)、(9)をiについて解いたものがLM曲線、
(10)をBP曲線と呼ぶ。
実際に解いたものを以下に示しておく。

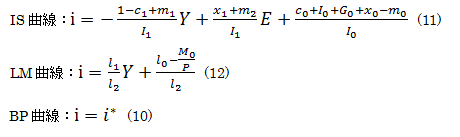
この3本の式には3つの外生変数i,Y,Eが存在するため、グラフにしようとすると3次元のグラフが必要になる。
しかし、ここで3次元のグラフを書こうとすればかなりややこしくなる。
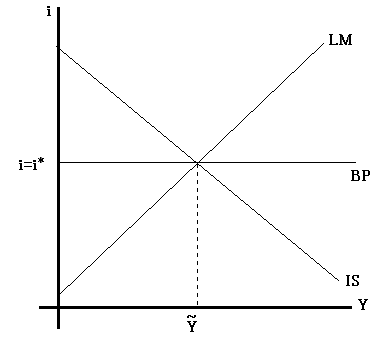
というわけで、Eは置いておいてiとYの2次元のグラフを用いて分析を行う。
IS曲線はYの係数が負であるので右下がり、LM曲線はYの係数が正なので右上がりとなる。
BP曲線はYの項が存在しないため、Y軸に対して水平になる。