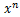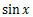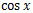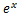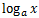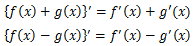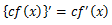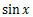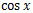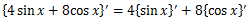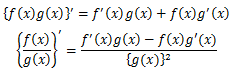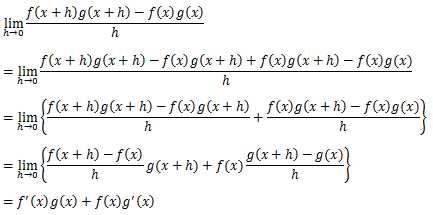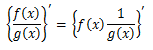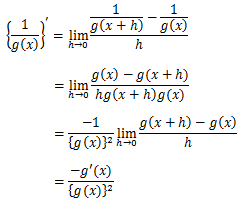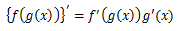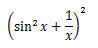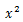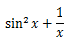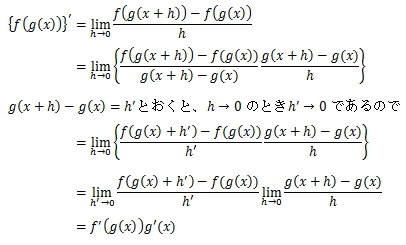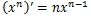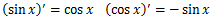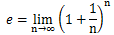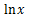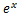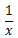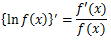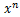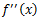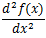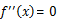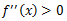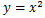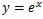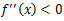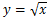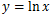ここでは、1変数関数の微分を紹介する。
様々な関数についての微分を紹介していくが、種類によって重要度は異なる。
- 微分の基本性質
- 積の微分、商の微分
- 合成関数微分
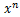 の微分
の微分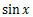 、
、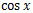 の微分
の微分- ネイピア数
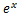 、
、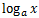 の微分
の微分- 対数微分法
- 2階微分
微分の基本性質
微分にはさまざまな公式がある。
それらを用いることにより、導関数の定義から求めようとも思えない複雑な関数も、
機械的な計算で求めることができる。
その為の公式をいくつか紹介する。
和の公式、差の公式
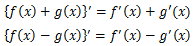
和の微分は微分の和という形となる。いわば微分の分配法則だ。
この公式により、関数の和と差を気にすることなく単項式の微分を行い、あとで足せば良いとわかる。
定数倍の微分
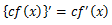
微分の際に定数倍になっているものはまとめて外に出すことが出来る。
これで、係数を気にすることなく微分を行えばよいことがわかる。
これら二つの公式を使えば、以下のような数式の微分は
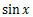
と
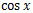
の微分が分かれば行うことが出来る。
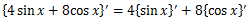
積の微分、商の微分
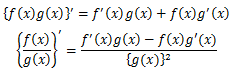
これが積の微分と商の微分の公式である。
積の微分は普通微分+微分普通という感じで、和であるのでどちらを微分にするかを悩む必要はない。
しかし、商の微分は分子が差であるので逆にすると結果が符号の分逆になってしまう。
というわけで、マイナスが付く方は分母の微分と覚えればよいと思う。
以下証明
積の微分
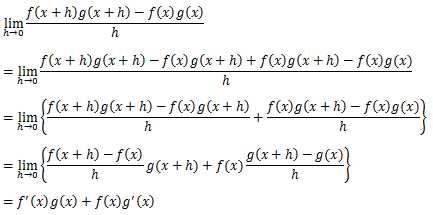
商の微分
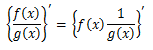
のように、積の微分のどちらかが分数関数であると考えれば同様に証明できる。
分数関数の微分の証明は以下に示す。
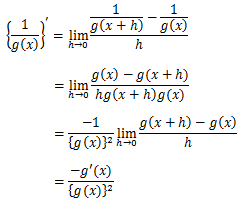
合成関数微分
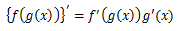
次は合成関数の微分だ。
式を見ると分かりにくいが、関数の変数の代わりにまた別の関数を用いているのが合成関数だ。
例えば、
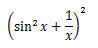
は、
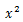
の変数に
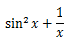
を代入したものだ。
経済学では使う機会が多く、必ず習得しておきたい技術だ。
以下証明
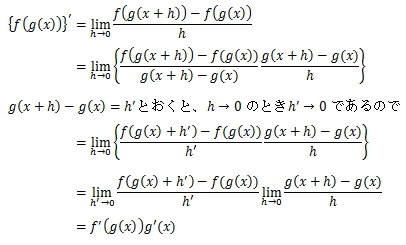
x^nの微分
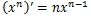
x^nは最も見かける機会の多い式だ。
これを微分できなければ、微分を習得したと言えることはないだろう。
nの値により普通の多項式だけでなく、無理式や分数式にも姿を変える。
その公式自体は単純で、指数部分と同じ値をかけて、指数部分から1を引けばよい。
このnは実は実数で成り立つのだが、それを証明するためには対数微分法というものを使わなければならない。
これはlogの微分の時に改めて紹介するので、ここではnが自然数の時の証明でお茶を濁しておく。
導関数の定義に沿った証明と積の微分の公式を使った証明の二つがある。
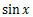 、
、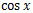 の微分
の微分
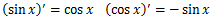
次は、いわゆる三角関数の微分の公式を紹介する。
正直な話、あまりこの微分が必要な場面を見かけないため、
証明を割愛して結果のみで終えておきたいと思う。
(きっちり証明しようとすれば多少面倒なことがあるというのもある)
ネイピア数
さて、ここから指数対数関数の微分に入っていくが、
その前に紹介しなければならない数がある。
それが、ネイピア数だ。
ネイピア数はeで表され、e=2.718281828……と続く無理数だ。
この数を利用すれば、指数対数の微分の公式は随分と綺麗な形になる。
その定義は以下のようなものだ。
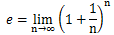
このネイピア数は指数対数において特殊な性質を持っている。
それは次項でしっかりと紹介する。
また、ネイピア数を底とした対数のことを自然対数と呼び、
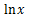
と表す。
他の底と異なる記号が与えられていることにその重要性がよく現れている。
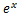 、
、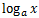 の微分
の微分
ここから本番の指数対数の微分に入っていく。
先にその微分の公式を以下にあげておく。
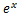
は微分しても変化しない。
これを前提としても同じようにeを求めることができる。
対数は自然対数であれば
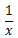
となり、非常に単純な式になる。
以下に証明を記しておく。
対数微分法
対数関数の微分と合成関数の微分を用いることで、次の式が証明される。
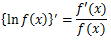
この公式を用いて微分を行うことを対数微分法という。
これを使えば、複雑で微分しようとも思えないような関数も比較的容易に微分できる。
というわけで例として、
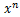
においてnが実数の場合を証明してみる。

2階微分
1度微分した関数を再び微分することを2階微分と呼ぶ。
2階微分の記号は
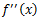
や、
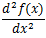
などと表記する。
通常の1階微分では接線の傾き(=変化率)がわかったが、
2階微分では、接線の傾きの変化率がわかるようになる。
つまり、グラフの増加具合がどのように変化するかを調べることができる。
例えば、
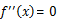
の場合、接線の傾きの変化率が0、つまり接線の傾きが常に一定ということになる。
よって、直線のグラフということになる。
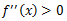
の場合、接線の傾きの変化率はどんどん大きくなっていくことになる。
よって、
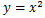
や
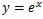
のような下に出っ張ったようなグラフになる。
これが財の生産関数に当てはまる場合、
規模に関して収穫逓増と呼ぶ。
逆に
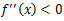
のときは、接線の傾きの変化率はどんどんと小さくなる。
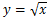
や
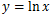
のような上に出っ張ったようなグラフになる。
生産関数に当てはまれば、
規模に関して収穫逓減と呼ぶ。
以下にそれぞれの場合をまとめておく。
最終更新:2013年07月20日 07:09