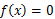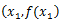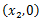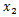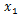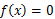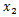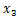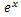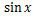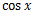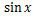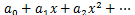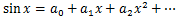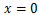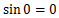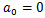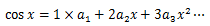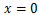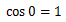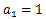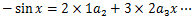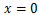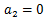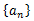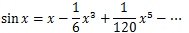ニュートン法、テイラー展開 - 経済学メモ

ここでは、ニュートン法とテイラー展開という異なる技法について紹介する。
経済学において使ってる場面を見たことがないので、あまり使われないのかもしれない。
しかし、せっかくなので紹介しておきたいと思う。

• ニュートン法
• テイラー展開

---

ニュートン法

ニュートン法は解がわからない方程式について、その解を求めようという方法である。
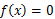
ある解が不明の方程式がある。ここで、そのグラフを考える。
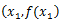
グラフ上の適当な点をとり、その接線を引く。
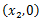
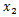
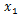
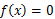
その接線とx軸の交点をとすると、そのはよりもの解の一つに近づく。
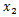
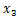
さらに、での接線を引いてを求める……この繰り返しで解の近似値を得られる。
極限的に繰り返せば、この方法で解を求めることができる場合がある。

テイラー展開

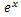
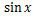
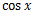
や、などは、普通の多項式と比べ少々扱いづらい。
そこでこれらの式を多項式で表すことができないか、ということで生み出されたのがテイラー展開だ。
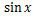
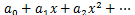
例としてを、という形で表せると仮定する。
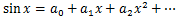
すると、①が成り立つ。
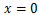
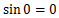
を代入するとより、
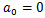
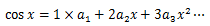
①を微分すると、②となる。
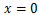
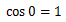
またを代入すると、より、
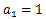
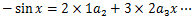
②を微分し、③を得る。
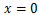
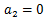
を代入し、を得る。

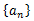
これを繰り返していくと係数の数列が決定できる。
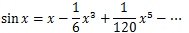
よってと表現できることになる。
これがテイラー展開と呼ばれる技法である。