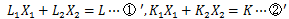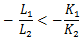ヘクシャー=オリーン理論 - 経済学メモ

リカードの比較生産費説の例では生産要素は労働のみだった。
ここでは、新たに生産要素として資本を追加する。
そのようなモデルにおいて、比較優位の源泉を探していく。

• ヘクシャー=オリーン定理
• リプチンスキー定理
• ヘクシャー=オリーン定理の証明

---

ヘクシャー=オリーン定理

リカードの比較生産費説では、まず最初に比較優位財の決定→
比較優位財に生産特化→比較優位財輸出→貿易利益発生、という流れだった。
それでは、そもそも最初に比較優位財を決定するための比較優位はどこから生まれるのだろうか？
言い換えれば、比較優位の源泉は一体どこに存在するのだろうか？
それを解明しようとした経済学者が、ヘクシャーとオリーンの2人である。
2人の研究により導かれた結果が「ヘクシャー=オリーンの定理」として現在に残っている。
そのヘクシャー=オリーンの定理(第1命題とも呼ばれる)の主張する内容は以下の通りだ。

ヘクシャー=オリーン定理

「各国は相対的に豊富に存在する生産要素を集約的に用いて作られる財の生産に比較優位を持つ」

ここで、資本集約財と労働集約財についての解説をしておく。
例として、衣服と自動車を1単位生産する為に必要な労働と資本の投入量が以下の表の通りだとする。

	衣服	自動車
労働	100	200
資本	100	400

ここで衣服は労働1単位に対して資本1単位を必要とする。
自動車であれば労働1単位に対して資本を2単位必要とする。
労働に対する資本の投入量は、相対的に見て自動車がより多くなっている。
逆に、資本に対する労働の投入量は、相対的に見て衣服がより多い。
このとき、自動車を資本集約財、衣服を労働集約財と呼ぶ。

以下ではモデルを用いてこの定理を証明する。
このモデルの仮定として、以下の8つを設定する。

1. 2国2財モデル(ドイツ、フランス、衣服、自動車)
2. 生産要素は資本と労働
3. 規模に関して収穫一定
4. 労働の国際移動は無し
5. 生産要素は完全利用される
6. 輸送費、関税等の貿易障壁はない(自由貿易)
7. 貨幣は財の交換のためだけに用いられ、交換比率も財の価格も一定
8. 各国の生産技術、選好は同一である(同一の財に関しては無差別)

リプチンスキー定理

ヘクシャー=オリーン定理を証明するために、まずこのリプチンスキー定理を証明する。
リプチンスキー定理とは、以下の様な定理である。

リプチンスキー定理

「(財の価格比率が一定のとき)一方の生産要素が増加した場合、その生産要素を集約的に用いる財の生産が増加し、他方の財生産は減少する」

この証明のためには、簡単な数式とグラフを用いる。
また、別枠としてより厳密な数式を使った証明も行う。
これは経済数学の知識を前提とするため、そちらを読んだあとに読むのが好ましい。
まず、資源制約式を定義する。

変数は全て正であるとする。
ここで、例えばは衣服部門の労働投入量を表す。
また賦存量とは、その国にもともとある生産要素の量である。
ここで①式②式は、仮定5より生産要素は完全利用されるので、
各部門の投入量の合計は賦存量に一致する。
したがって①式②式では不等号は成り立たないので、以下のようになる。

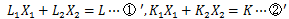
ここで、2つの財のうち自動車を資本集約財、衣服を労働集約財とする。
衣服は労働集約財なので、単位当たりの労働投入量と資本投入量の比が、
自動車の自動車の単位当たり労働投入量と資本投入量の比より大きくなる。
したがって、が成り立つ。
これを変形して、……③を得る。
①'式②'式をについて解くと、①'式よりとなり、
②'式よりを得る。
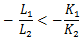
③式よりであるので、①"式と②"式を平面にグラフにすると以下のようになる。

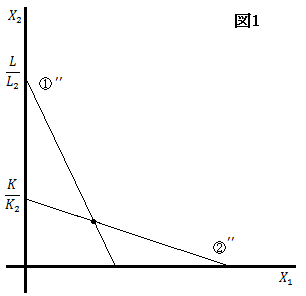
それぞれのグラフは各国の労働、資本の賦存量と単位当たり投入量と各財の生産量の関係を表す。
2本のグラフの交点を、均衡生産水準と呼ぶ。
この均衡生産水準において、実際に各財の生産が行われることになる。
また、外生変数であるの値によっては、2本のグラフが交わらないことがある。
しかし、そのような場合では生産が行われない。
各財の生産量はこのグラフ上のいずれかに必ず存在する。
さらに、労働と資本の両方の生産要素を投入して初めて財が生産されるため、,は1組しか存在しない。
なので、2本のグラフの交点(=等しい,の組が存在する)において生産量が決定される。

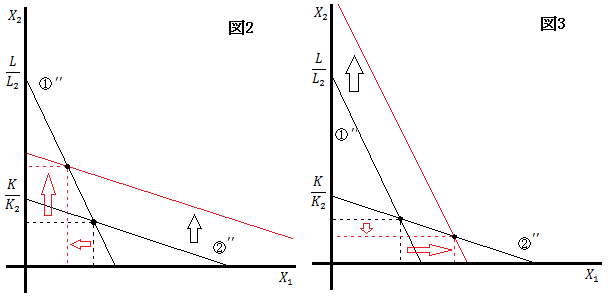
ここで、資本賦存量Kが増加したとする。
すると、下図2のように②"式が上方にシフトする。
それに従って均衡生産水準も移動し、資本集約財の生産が増加し、労働集約財の生産が減少する。
同様に労働賦存量Lが増加すると、下図3のようにの生産が増加し、の生産が減少する。
これによって、リプチンスキー定理の証明が完了した。

ヘクシャー=オリーン定理の証明

資本賦存量Lが増加したあとの賦存量をL'とする。
これを一国の資本賦存量が変化したと考えるのではなく、
比較的資本賦存量の少ないLを持つA国、比較的多いL'を持つB国の2国あると考えてみる。
A国を資本希少国(労働豊富国)、B国を資本豊富国(労働希少国)と呼ぶ。
ここでA国をフランス、B国をドイツと名前を付けておく。
A点での生産量がフランスの生産量,となり、同様にB国の生産量がドイツの生産量,となる。
ここで、2財の生産量の比である相対生産量、を考えてみる。
図1より、、であるので、が成り立つ。

軸として価格と生産量を用いる代わりに、2財の価格比と生産量比を軸とした平面を考える。
その平面上での需要曲線、供給曲線を相対需要曲線、相対供給曲線と呼ぶ。
相対供給曲線では、自動車の価格が相対的に上昇すると、自動車の生産量が相対的に増加する。
また軸が価格比であるため、が相対的に減少した場合も同様にが相対的に増加する。
,の関係も同様であるので、自動車と衣服の価格比が大きくなると、自動車と衣服の生産量比が大きくなる。
よって、下図4のように相対供給曲線は右上がりとなる。
が常に成り立っているので、フランスの相対供給曲線は常にドイツの相対供給曲線の左側に存在する。

相対需要曲線でも同じように考えることができ、右下がりの曲線となる。
また仮定8より国ごとの選好の違いは存在しないため、両国ともに同じ需要曲線に直面する。
したがって、相対需要曲線は1本のみとなり下図5のようなグラフになる。

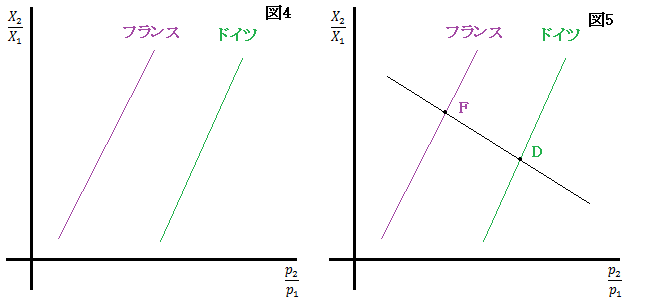
下図右において、フランスとドイツのそれぞれの均衡点を見てみる。
すると、ドイツの均衡点Dはフランスの均衡点Fに比べて右側にあり、下側にある。
つまり、ドイツにおける自動車の生産量は相対的にフランスより多く、価格もフランスより安くなる。
逆にフランスにおける衣服の生産量は相対的にドイツより多く、価格もドイツより安いという事も出来る。
ここで、ドイツは資本集約国でフランスは労働集約国だと仮定していて、自動車は資本集約財で衣服は労働集約財だった。
したがって、それぞれの生産要素を豊富に所有する国が、その生産要素を集約的に用いて生産される財について価格的な優位性、すなわち比較優位を持つということが出来る。
よって、ヘクシャー=オリーン定理が証明された。