- 方程式体系
- 名目値と実質値
- 投資需要の決定
- 貨幣需要の決定
- IS-LMモデル
△
方程式体系
IS-LMモデルでは以下の9本の方程式を用いる。
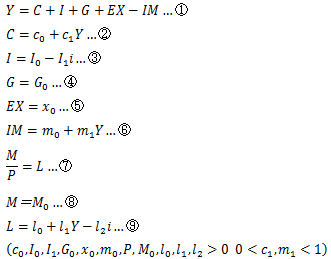
この内①〜⑥式がIS曲線となり、⑦〜⑨式がLM曲線となる。
変数のうちモデルの外部から与えられる外生変数は

で、
モデルの内部で決定される内生変数はY,C,I,G,EX,IM,M,L,iの9つである。
名目値と実質値
⑦式に登場する外生変数Pは物価を表す。
今回は短期でのモデルなのでPを固定して考える。
Mは名目貨幣供給量(マネーサプライ)を表し、Lは実質貨幣需要を表す。
⑦式は実質の貨幣市場の需給均衡式を表すことになる。
ここに登場する名目と実質にはどのような違いがあるのだろうか。
例としてコーヒーで考える。
1900年頃ではコーヒーは1杯1円ほどだった。
しかし2013年現在では1杯500円ほどだろう。
また、1900年も2013年ももちろん1万円は同じ1万円である。
これは1円を単位として、どちらも1円が1万あるという意味である。
ここで単位を1円からコーヒー1杯に変更してみる。
1900年ではコーヒー1万杯買うことができるが、2013年には20杯しか買うことができない。
上の例で単位を1円として測るのが名目で、コーヒーで測る場合が実質である。
コーヒー1杯の値段が物価(物の価格)であり、1900年と2013年では物価が上昇しているためコーヒーの価格が異なる。
名目値と実質値の関係は名目値/物価=実質値である。
投資需要の決定
投資をするには多くの資金が必要となる。
その資金をそのまま出せるような企業ならばよいのかもしれないが、ほとんどの企業にそのような余裕はない。
したがってほとんどの会社は投資を行う際に銀行などから融資を受けて借金をして投資の資金にする。
そこで問題となってくるのが利子率だ。
借りたお金はもちろん返さねばならず、さらに利子も支払わなければならない。
その利子がどれくらいなのかを決めるのが利子率である。
この利子率がどれくらいなのかによって企業は投資するプロジェクトを決定することになる。
例えば期待収益率(投資額に対して何%の利益が出るか)が10%のプロジェクトAと20%のプロジェクトBがあるとする。
プロジェクトに必要な投資額が10億円だとすると、それぞれの収益は1億円と2億円である。
ここで利子率が15%だとする。この場合、10億円借りれば1億5000万円を利子として追加で返す必要がある。
この時に10億円借りてプロジェクトAに投資したとすると1億-1億5000万=-5000万円となり赤字になってしまう。
企業がわざわざ赤字になるとわかっているプロジェクトに乗り出すことは考えられず、このプロジェクトは行われない。
プロジェクトBに投資した場合、2億-1億5000万=5000万円と黒字が出る。
したがって企業はこちらのプロジェクトBを行うだろう。
片方だけしかプロジェクトが行われないため、総投資額は10億円である。
利子率が突如8%まで下がったとする。10億円の利子は8000万円まで下がった。
この場合ではプロジェクトBはもちろんプロジェクトAも1億-8000万=2000万円と黒字になる。
したがってどちらのプロジェクトも行われることになり、総投資額は20億円になる。
逆に利子率が25%に上昇したとしたらどうだろうか。10億円の利子は2億5000万円にもなる。
プロジェクトAはもちろん赤字だが、プロジェクトBも2億-2億5000万=-5000万円と赤字だ。
このような状態ではどちらのプロジェクトも行われず、総投資額は0円となる。
このように利子率iと投資額Iは負の関係を持っているといえる。
(図1)
上の例ではプロジェクトが2つしかなかったため、上図のグラフもいびつになっている。
しかし現実では行うことのできるプロジェクトは無数にある。
そのプロジェクトを期待収益率の高い順に並べた下のグラフを投資の限界効率表と呼ぶ。
上の図1もプロジェクトが二つしかないが投資の限界効率表と呼ぶことができる。
企業は利子率と期待収益率を勘案して、どのプロジェクトに投資するかを決定している。
(図2)
貨幣需要の決定
⑨式は貨幣需要についての式である。
この式では貨幣需要Lが利子率iと負の関係になっている。
これはどのような事実から導かれるのだろうか。
例えばある人が資産を1億円持っているとする。
その資産は貨幣、債券、株式等々と様々な形で持つことができる。
しかしここでは、資産を貨幣か債券かのどちらかで持つと仮定する。
貨幣はすぐに使えるという便利さを持つ反面、資産をさらに増やす効果はない。
これに対して債券はすぐに使うことが出来ないが、償還時に利子率に応じた利子で利益を得ることができる。
ここで、利子率が上昇したとする。
利子率が上昇するということは債券の償還額が増加するということだ。
それによって資産を債券として持つインセンティブが高まり、貨幣需要は減少する。
逆に利子率が低下した場合には、債券を持つインセンティブが小さくなり、貨幣需要は上昇する。
IS-LMモデル
IS-LMモデルに登場するIS曲線とLM曲線はYi平面(横軸Y、縦軸iの平面)上に存在する。
IS曲線は財市場を均衡させる生産量Yと利子率iの組み合わせを表す。
LM曲線は貨幣市場を均衡させる生産量Yと利子率iの組み合わせを表す。
つまりIS曲線とLM曲線の交点は、財市場と貨幣市場のどちらもを均衡させる生産量と利子率の組み合わせを表すことになる。
市場の調節機能により、この均衡点に向かって生産量Yと利子率iが動いていく。
では実際にIS曲線とLM曲線を求めてみる。
①~⑥式を1本の式にまとめると、

となる。
これをさらにiについて解くと、

となり、これがIS曲線である。
同様に⑦~⑨式をiについて解くと、

が得られ、これがLM曲線だ。
Yの係数について見てみると、IS曲線は負でLM曲線は正である。
したがってIS曲線は右下がり、LM曲線は右上がりとなる。
これをグラフに図示すると以下のようになる。
(図3)
これを用いて分析を行いたくなる気持ちをぐっと抑えて、次のステップへと足を進めよう。
本格的な分析はその先になる。
最終更新:2013年12月03日 12:41