メモ帳ブログ @ wiki

ラグランジュの未定乗数法

最終更新：2011年04月11日 00:56

nina_a

- view

管理者のみ編集可

ラグランジュの未定乗数法

概要

　ラグランジュの未定乗数法とは、D次元の変数 $\mathbf{x}=\left\{x_1, x_2, \cdots, x_D\right\}$ に対し、q個の制約条件（束縛条件とも） $g_i(\mathbf{x})=0\quad(i=1,2,\cdots,q)$ の下で関数 $f(\mathbf{x})$ を最適化する（最大化、最小化）ために用いる数学的手法である。
　まず、ラグランジュ乗数 $\lambda_i \neq 0\quad(i=1,2,\cdots,q)$ を導入し、次にラグランジュ関数
$L(\mathbf{x}, \lambda)\equiv f(\mathbf{x}) + \sum_{i=1}^{q}\lambda_ig_i(\mathbf{x})$
を導入する。
　このとき、
$\begin{cases}\frac{\partial}{\partial \mathbf{x}}L = 0 \\ \frac{\partial}{\partial \lambda}L = 0 \end{cases}$
の連立方程式を解くことによって解の候補が得られる。

例

　関数 $f(x,y)=x+y$ を制約条件 $g(x,y)=x^2+y^2-1=0$ の下で最大化する問題を考える。
　まず、
$L(x,y,\lambda) = f(x,y)+\lambda g(x,y) = x+y+\lambda(x^2+y^2-1)$
とする。ここで、
$(a)\qquad \dfrac{\partial}{\partial x}L = 1 + 2\lambda x = 0$
$(b)\qquad \dfrac{\partial}{\partial y}L = 1 + 2\lambda y = 0$
$(c)\qquad \dfrac{\partial}{\partial \lambda}L = x^2+y^2-1 = 0$
を解けばよい。
　(a)-(b)より、 $2\lambda(x-y)=0$ で、 $\lambda\neq 0$ であるから $x=y$ が成り立つ。これを(c)に代入して、
$2x^2-1=0$
　よって、
$x=\pm\dfrac{1}{\sqrt{2}},\;y=\pm\dfrac{1}{\sqrt{2}}$ (複号同順)
　この値をfに入れて計算すると、最大は $x=y=\frac{1}{\sqrt{2}}$ で $f=\frac{2}{\sqrt{2}}$ となる。

解説

１． $\nabla g$ が $g(x)=0$ に対して常に垂直であることの説明

　まず $g(x)=0$ 上の点、 $x$ と $x+\varepsilon$ を考える。 $\varepsilon$ の大きさは微小であり、これら2点は互いに近傍であるとする。この時、 $x$ の周りの $g(x)$ のテイラー展開より
$g(x+\varepsilon)=g(x)+\varepsilon^\top(\nabla g)+O(|\varepsilon|^2)$
が成り立つ。ここで $\nabla g$ は $g$ の勾配（グラディエント）を表しており、
$\nabla g = \left[\dfrac{\partial}{\partial x_1}g\quad\dfrac{\partial}{\partial x_2}g\quad\cdots\quad\dfrac{\partial}{\partial x_D}g\right]$
である。また $O$ はランダウの記号である。

※ここでは、テイラー展開について言及しません。

　 $x$ と $x+\varepsilon$ はともに $g(x)=0$ 上の点であったから、
$0=\varepsilon^\top(\nabla g)+O(|\varepsilon|^2)$
の関係が成り立つ。ここで $\varepsilon\rightarrow 0$ とすると、
$0=\varepsilon^\top(\nabla g)$
である。
　また、 $\varepsilon\rightarrow 0$ の時 $\varepsilon$ は点 $x$ における接線であるから、制約式の勾配 $\nabla g$ は曲面 $g(x)=0$ に対して常に垂直であることが分かる。

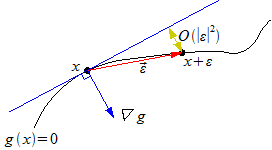
図・∇gはg(x)=0と常に垂直である（EPS）

２．未定乗数 $\lambda\neq0$ が存在することの説明

　制約条件 $g(x)=0$ 上で、関数 $f(x)$ が最大となる点を $\bar x$ とおく。 $\bar x$ においては $\nabla f$ も $g(x)=0$ に対して垂直となる。もし、垂直でないと仮定すると、下の図のようにさらに $f(x)$ が大きくなる方向にxが移動できるからである。

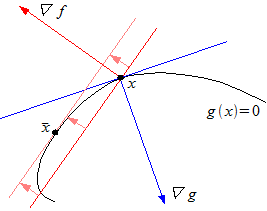
図・∇gと∇fが平行で無い状態（EPS）

　よって、 $\nabla f\parallel\nabla g$ であることが分かる。これは、すなわち
$\nabla f+\lambda\nabla g=0\qquad(\lambda\neq0)$
という関係が成り立つ。この $\lambda$ がラグランジュ乗数である。

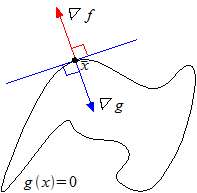
図・∇gと∇fが平行になる点が解の候補である（EPS）

３．ラグランジュ関数 $L$ を偏微分し連立方程式を解くと解候補が求まることの説明

　ラグランジュ関数 $L$ は以下のように定義した。
$L(\mathbf{x}, \lambda)\equiv f(\mathbf{x}) + \sum_{i=1}^{q}\lambda_ig_i(\mathbf{x})$
　まず、根本となる制約条件は $\frac{\partial}{\partial \lambda}L=0\quad\cdots(1)$ から導くことが出来る。
　次に、解説２．で得られた $\nabla f+\lambda\nabla g=0\qquad(\lambda\neq0)$ という条件は、 $\frac{\partial}{\partial \mathbf{x}}L=0\quad\cdots(2)$ から導くことが出来る。
　(1)式から1個の方程式が、(2)式からD個の方程式が得られる。計(D+1)個の方程式が得られるので、これを解けば $\bar x$ の候補と $\lambda$ を求めることが出来る。 $\bar x$ の候補のみを求めればよい場合、 $\lambda$ を消去してから解を求めることが出来る（ $\lambda$ を求める必要がない）。これが未定乗数という名の由来である。

制約に不等式制約を含む場合

　続いて、制約に不等式制約を含む場合に、ラグランジュの未定乗数法を適用する。すなわち、q個の等式制約とr個の不等式制約がある場合を考える。なお、不等式制約は、
$h_1(\mathbf{x})\leq 0,\;h_2(\mathbf{x})\leq 0,\;\cdots,\;h_r(\mathbf{x})\leq 0$
のように不等号の向きを統一しておく。

有効制約と無効制約

　不等式制約は有効制約（アクティブ制約）と無効制約（ノンアクティブ制約）に分けることが出来る。

有効制約: 最適解 $\mathbf{x}^*$ において等号が成り立っている。すなわち、 $h_i(\mathbf{x}^*)=0$ であるもの。
無効制約: 最適解 $\mathbf{x}^*$ において不等号が成り立っている。すなわち、 $h_i(\mathbf{x}^*)<0$ であるもの。

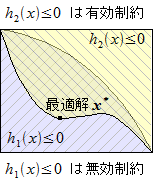
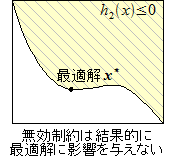
図・有効制約と無効制約

　もし、不等式制約が有効制約か無効制約かを予め知ることが出来れば、不等式制約付き問題は等式制約付き問題と同様に扱うことが出来る。すなわち、有効制約を等式制約として扱い、無効制約を無視する。
　不等式制約のうち、有効制約の番号の集まりを $A$ とし、無効制約の集まりを $\bar A$ とする。
$A=\{i|g_i(\mathbf{x}^*)=0\}$
$\bar A=\{i|g_i(\mathbf{x}^*)<0\}$
　すると、ラグランジュ関数は、有効制約のみを等式制約として考えればよいのだから、
$L(\mathbf{x},\lambda,\mu)=f(\mathbf{x})+\sum_{i=1}^q\lambda_ig_i(\mathbf{x})+\sum_{i\in A}\mu_ih_i(\mathbf{x})$
と置くことが出来る。
　ここで注意すべき事は、ラグランジュ乗数 $\mu$ の取り得る値の範囲である。等式制約では $\nabla f\parallel\nabla g$ が解の候補である条件であったが、不等式制約では $\nabla f$ と $\nabla h$ の向きも考える必要があるため、 $\mu$ の取り得る値の範囲は制限される。
　例えば、最小化の場合には、

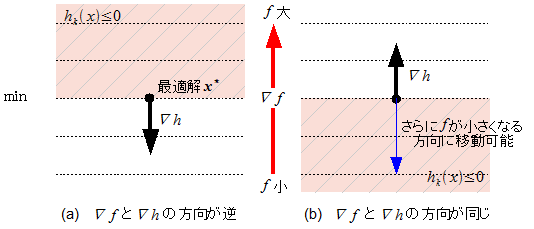
図・∇fと∇h（最小化）

上図から、最小化の際には $\nabla f$ と $\nabla h$ が逆向きである必要があることがわかる。よって、
$\nabla f+\mu\nabla h=0\qquad(\mu>0)$
である。
　次に最大化についてみてみると、

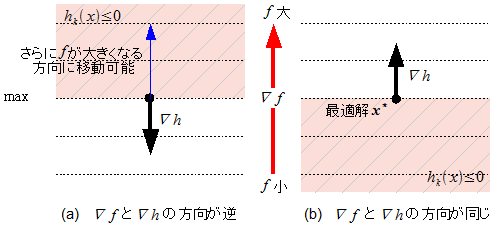
図・∇fと∇h（最大化）

上図から、
$\nabla f+\mu\nabla h=0\qquad(\mu<0)$
であることが分かる。

※ここでは最小化、最大化の2つの場合によってラグランジュ乗数 $\mu$ の正負を変えたが、ラグランジュ関数を変えることもある。
　つまり、最小化するときのラグランジュ関数を
$L(\mathbf{x},\lambda,\mu)=f(\mathbf{x})+\sum_{i=1}^q\lambda_ig_i(\mathbf{x})+\sum_{i\in A}\mu_ih_i(\mathbf{x})$
　最大化するときの関数を
$L(\mathbf{x},\lambda,\mu)=f(\mathbf{x})+\sum_{i=1}^q\lambda_ig_i(\mathbf{x})-\sum_{i\in A}\mu_ih_i(\mathbf{x})$
と置く。このとき、 $\mu$ は最小化・最大化に関わらず $\mu>0$ である。

※不等式制約の不等号の向きによっても、 $\mu$ の不等号の向きは変化するので注意。

相補性条件

　ここまで、有効制約と無効制約が予め分かっているという前提で話を進めてきたが、実際はそうではない。この問題に対して、相補性条件と呼ばれる条件を導入する。

相補性条件: $\mu_kh_k(\mathbf{x})=0$

　この条件を導入することによって、有効制約と無効制約を区別する必要がなくなる。すなわち、ラグランジュ関数は以下のように書くことが出来る。
$L(\mathbf{x},\lambda,\mu)=f(\mathbf{x})+\sum_{i=1}^q\lambda_ig_i(\mathbf{x})+\sum_{i=1}^r\mu_ih_i(\mathbf{x})$
　もし、 $h_k$ が有効制約であったとすると、最適解 $\mathbf{x}^*$ では $h_k(\mathbf{x}^*)=0$ であるため、この相補性条件によって乗数 $\mu_k$ が制限されることは無い。しかし、 $h_k$ が無効制約の場合は $h_k&lt;0$ であるため $\mu_k=0$ となる。そのため、ラグランジュ関数の $\mu_kh_k(\mathbf{x})\quad(k\in \bar A)$ は無視することが出来る。

KKT条件

　以上をまとめると、不等式制約付き最適化問題（最小化の場合）

$\begin{matrix} \displaystyle\min_{\mathbf{x}} & f(\mathbf{x}) &&& \\ \mathit{s.t.} & g_1(\mathbf{x})=0,& g_2(\mathbf{x})=0,& \cdots,& g_q(\mathbf{x})=0, \\ </p> <pre>& h_1(\mathbf{x})\leq0,& h_2(\mathbf{x})\leq0,& \cdots,& h_r(\mathbf{x})\leq0 </pre> <p>\end{matrix}$

は、ラグランジュ関数
$(1)\qquad L(\mathbf{x},\lambda,\mu)=f(\mathbf{x})+\sum_{i=1}^q\lambda_ig_i(\mathbf{x})+\sum_{i=1}^r\mu_ih_i(\mathbf{x})$
を、
$(2)\qquad h_k(\mathbf{x})\leq 0$
$(3)\qquad \mu_k\geq 0$
$(4)\qquad \mu_kh_k(\mathbf{x})=0$
の条件の下で最適化してやればよいということが分かる。これらの条件（２）、（３）、（４）をKKT条件（カルーシュ・キューン・タッカー条件、Karush-Kuhn-Tucker condition）という。

※最適化問題では、目的関数を最小化、制約条件は $h_k(x)\leq0$ とするのが標準的です。もちろん、問題の定式化にはいろいろありますが。

主問題と双対問題

　ラグランジュ関数は $L(\mathbf{x},\lambda,\mu)=f(\mathbf{x})+\sum_{i=1}^q\lambda_ig_i(\mathbf{x})+\sum_{i=1}^r\mu_ih_i(\mathbf{x})$ と表された。ここで最適解を $\mathbf{x}^*$ 、最適解における $\lambda, \mu$ の値をそれぞれ $\lambda^*, \mu^*$ とする。

すると $L(\mathbf{x}^*, \lambda^*, \mu^*)=f(\mathbf{x}^*)$ であるから、 $L(\mathbf{x}^*, \lambda^*, \mu^*)\leq f(\mathbf{x})\qquad\cdots(a)$ となる。
また、 $L(\mathbf{x}^*, \lambda, \mu)=f(\mathbf{x}^*)+\sum_{i=1}^r\mu_ih_i(\mathbf{x}^*)$ であり、 $\mu_k>0, h_k(\mathbf{x}^*)\leq 0$ より $\mu_ih_i(\mathbf{x}^*)\leq 0$ であるから、 $L(\mathbf{x}^*, \lambda, \mu)\leq f(\mathbf{x}^*) = L(\mathbf{x}^*, \lambda^*, \mu^*)\qquad\cdots(b)$ である。
さらに、制約無し最小化問題 $\phi(\lambda, \mu)\equiv \min_\mathbf{x} L(\mathbf{x}, \lambda, \mu)$ を定義する。これは制約有り最小化問題 $\min_{\mathbf{x}} L(\mathbf{x},\lambda,\mu)\;\mathit{s.t.}\;\cdots$ よりも、制約がない分値を小さくすることが出来る。つまり、 $\phi(\lambda, \mu)\leq L(\mathbf{x}^*, \lambda, \mu) \qquad\cdots(c)$ である。

　以上(a),(b),(c)より、
$\phi(\lambda, \mu)\leq L(\mathbf{x}^*, \lambda^*, \mu^*)\leq f(\mathbf{x})$
であることが分かる。これまで、 $f(\mathbf{x})$ を最小化することによって $\mathbf{x}^*, \lambda^*, \mu^*$ を求めてきたが、 $\phi(\lambda, \mu)$ を最大化することによっても $\mathbf{x}^*, \lambda^*, \mu^*$ を求めることが出来る。前者の最小化問題を主問題、後者の最大化問題を双対問題と言う。