Using Uninitialized Memory for Fun and Profits - お気軽便利に未初期化メモリを使う
| 開始日 | 2008年12月9日(火) |
| 翻訳完了日 | |
| 最終更新日 | 2009年06月05日 |
はじめに
愛読しているブログ:Radium Softwareで、「未初期化メモリを使う」という記事が載っていました。何でも、《定義時には不定値が入っている配列を2つ組み合わせることで、初期化しないままでも問題なく使用できる方法》なのだそうで。
何だかとても面白そうなので、勉強がてら参照元サイトを訳してみようと思いました。
原著
research!rsc: 「Using Uninitialized Memory for Fun and Profit」
http://research.swtch.com/2008/03/using-uninitialized-memory-for-fun-and.html
http://research.swtch.com/2008/03/using-uninitialized-memory-for-fun-and.html
注意
- もともと個人利用を目的として日本語化したために、けっこう意訳している部分があります。「意味分からないよ」とか「おかしいんじゃない?」とかいうのがあれば、オリジナルを参照するか、コメントで質問してください(がんばって調べます)。
また、オリジナルのサイトには20近く(2008/12/09現在)のコメントが付いています。この内容は訳していませんので、全体理解のためにはそちらも見ておくことをお勧めします。
用語
訳文に出てくる各語に対応する原文と、その意味を以下に記します。
| 訳語 | 原文 | 意味 |
更新履歴
- 2008/12/09 作成開始
訳文
Friday, March 14, 2008
Using Uninitialized Memory for Fun and Profit
お気軽便利に未初期化メモリを使う方法
This is the story of a clever trick that's been around for at least 35 years, in which array values can be left uninitialized and then read during normal operations, yet the code behaves correctly no matter what garbage is sitting in the array. Like the best programming tricks, this one is the right tool for the job in certain situations. The sleaziness of uninitialized data access is offset by performance improvements: some important operations change from linear to constant time.
この記事では、未初期化(しかもゴミだらけ)の配列を正しく取り扱うための、35年も前からある賢いトリック(clever trick)を紹介するよ。このプログラミングトリックは特定の状況下では優れたツールになるんじゃないかな。未初期化データへのアクセスという危険性はパフォーマンス向上によって相殺される、というのが特徴だ。遅延が線形から定数時間に変わる、というね。
Alfred Aho, John Hopcroft, and Jeffrey Ullman's 1974 book The Design and Analysis of Computer Algorithms hints at the trick in an exercise (Chapter 2, exercise 2.12):
Alfred Aho、John Hopcroft、Jeffrey Ullmanらによる1974年に刊行された書籍「The Design and Analysis of Computer Algorithms (邦訳:アルゴリズムの設計と解析)」では、演習問題で本トリックのヒントが出ているよ。第2章の問題2.12だ。
Develop a technique to initialize an entry of a matrix to zero the first time it is accessed, thereby eliminating the O(||V||2) time to initialize an adjacency matrix.
行列の各要素にアクセスする前に0初期化しておくテクニックを考えよ。それによって隣接行列の初期化にかかるO(||V||2)の時間を排除できるためだ。
Jon Bentley's 1986 book Programming Pearls expands on the exercise (Column 1, exercise 8; exercise 9 in the Second Edition):
1986年にJon Bentleyが著した書籍「Programming Pearls(邦題:珠玉のプログラミング)」にて示された例題だ(第1章、例題8。第2章では例題9)。
One problem with trading more space for less time is that initializing the space can itself take a great deal of time. Show how to circumvent this problem by designing a technique to initialize an entry of a vector to zero the first time it is accessed. Your scheme should use constant time for initialization and each vector access; you may use extra space proportional to the size of the vector. Because this method reduces initialization time by using even more space, it should be considered only when space is cheap, time is dear, and the vector is sparse.
より大きな空間を短時間で取り扱う際の問題として、自分自身の領域を初期化するときに多量の時間を消費してしまうことがあるよ。そこで配列内の要素に初めてアクセスされる際にゼロ初期化するという、技術的デザインによる問題の回避方法を紹介しよう。この仕組みは初期化・配列アクセスに定時間しか必要としない。ただし配列のサイズに比例した領域は追加で必要になるけれどね。なぜって、この方法は領域を犠牲にして初期化時間を減らすことが目的だから。つまり、領域は豊富にあって時間は貴重で、そして配列は疎(sparse)であるときに使用すべきだって言うこと。
Aho, Hopcroft, and Ullman's exercise talks about a matrix and Bentley's exercise talks about a vector, but for now let's consider just a simple set of integers.
One popular representation of a set of n integers ranging from 0 to m is a bit vector, with 1 bits at the positions corresponding to the integers in the set. Adding a new integer to the set, removing an integer from the set, and checking whether a particular integer is in the set are all very fast constant-time operations (just a few bit operations each). Unfortunately, two important operations are slow: iterating over all the elements in the set takes time O(m), as does clearing the set. If the common case is that m is much larger than n (that is, the set is only sparsely populated) and iterating or clearing the set happens frequently, then it could be better to use a representation that makes those operations more efficient. That's where the trick comes in.
Preston Briggs and Linda Torczon's 1993 paper, “An Efficient Representation for Sparse Sets,” describes the trick in detail. Their solution represents the sparse set using an integer array named dense and an integer n that counts the number of elements in dense. The dense array is simply a packed list of the elements in the set, stored in order of insertion. If the set contains the elements 5, 1, and 4, then n = 3 and dense[0] = 5, dense[1] = 1, dense[2] = 4:
One popular representation of a set of n integers ranging from 0 to m is a bit vector, with 1 bits at the positions corresponding to the integers in the set. Adding a new integer to the set, removing an integer from the set, and checking whether a particular integer is in the set are all very fast constant-time operations (just a few bit operations each). Unfortunately, two important operations are slow: iterating over all the elements in the set takes time O(m), as does clearing the set. If the common case is that m is much larger than n (that is, the set is only sparsely populated) and iterating or clearing the set happens frequently, then it could be better to use a representation that makes those operations more efficient. That's where the trick comes in.
Preston Briggs and Linda Torczon's 1993 paper, “An Efficient Representation for Sparse Sets,” describes the trick in detail. Their solution represents the sparse set using an integer array named dense and an integer n that counts the number of elements in dense. The dense array is simply a packed list of the elements in the set, stored in order of insertion. If the set contains the elements 5, 1, and 4, then n = 3 and dense[0] = 5, dense[1] = 1, dense[2] = 4:
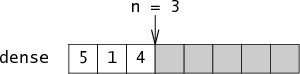
Together n and dense are enough information to reconstruct the set, but this representation is not very fast. To make it fast, Briggs and Torczon add a second array named sparse which maps integers to their indices in dense. Continuing the example, sparse[5] = 0, sparse[1] = 1, sparse[4] = 2. Essentially, the set is a pair of arrays that point at each other:
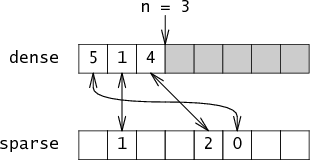
Adding a member to the set requires updating both of these arrays:
add-member(i):
dense[n] = i
sparse[i] = n
n++
It's not as efficient as flipping a bit in a bit vector, but it's still very fast and constant time.
To check whether i is in the set, you verify that the two arrays point at each other for that element:
To check whether i is in the set, you verify that the two arrays point at each other for that element:
is-member(i):
return sparse[i] < n && dense[sparse[i]] == i
If i is not in the set, then it doesn't matter what sparse[i] is set to: either sparse[i] will be bigger than n or it will point at a value in dense that doesn't point back at it. Either way, we're not fooled. For example, suppose sparse actually looks like:
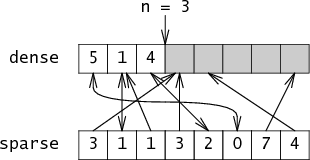
Is-member knows to ignore members of sparse that point past n or that point at cells in dense that don't point back, ignoring the grayed out entries:
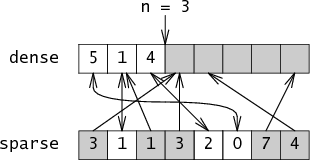
Notice what just happened: sparse can have any arbitrary values in the positions for integers not in the set, those values actually get used during membership tests, and yet the membership test behaves correctly! (This would drive valgrind nuts.)
Clearing the set can be done in constant time:
Clearing the set can be done in constant time:
clear-set():
n = 0
Zeroing n effectively clears dense (the code only ever accesses entries in dense with indices less than n), and sparse can be uninitialized, so there's no need to clear out the old values.
This sparse set representation has one more trick up its sleeve: the dense array allows an efficient implementation of set iteration.
This sparse set representation has one more trick up its sleeve: the dense array allows an efficient implementation of set iteration.
iterate():
for(i=0; i<n; i++)
yield dense[i]
Let's compare the run times of a bit vector implementation against the sparse set:
| Operation | Bit Vector | Sparse set |
| is-member | O(1) | O(1) |
| add-member | O(1) | O(1) |
| clear-set | O(m) | O(1) |
| iterate | O(m) | O(n) |
The sparse set is as fast or faster than bit vectors for every operation. The only problem is the space cost: two words replace each bit. Still, there are times when the speed differences are enough to balance the added memory cost. Briggs and Torczon point out that liveness sets used during register allocation inside a compiler are usually small and are cleared very frequently, making sparse sets the representation of choice.
Another situation where sparse sets are the better choice is work queue-based graph traversal algorithms. Iteration over sparse sets visits elements in the order they were inserted (above, 5, 1, 4), so that new entries inserted during the iteration will be visited later in the same iteration. In contrast, iteration over bit vectors visits elements in integer order (1, 4, 5), so that new elements inserted during traversal might be missed, requiring repeated iterations.
Returning to the original exercises, it is trivial to change the set into a vector (or matrix) by making dense an array of index-value pairs instead of just indices. Alternately, one might add the value to the sparse array or to a new array. The relative space overhead isn't as bad if you would have been storing values anyway.
Briggs and Torczon's paper implements additional set operations and examines performance speedups from using sparse sets inside a real compiler.
Another situation where sparse sets are the better choice is work queue-based graph traversal algorithms. Iteration over sparse sets visits elements in the order they were inserted (above, 5, 1, 4), so that new entries inserted during the iteration will be visited later in the same iteration. In contrast, iteration over bit vectors visits elements in integer order (1, 4, 5), so that new elements inserted during traversal might be missed, requiring repeated iterations.
Returning to the original exercises, it is trivial to change the set into a vector (or matrix) by making dense an array of index-value pairs instead of just indices. Alternately, one might add the value to the sparse array or to a new array. The relative space overhead isn't as bad if you would have been storing values anyway.
Briggs and Torczon's paper implements additional set operations and examines performance speedups from using sparse sets inside a real compiler.
( - )
