center_math @ ウィキ
center_math @ ウィキ

暗号

以下、平文:P,暗号文:C,暗号化鍵:e,復合鍵:dとする


単一換字式暗号

シーザー暗号


A=0,B=1,...,Z=25
とおいたとき、+3を行うことで暗号化する。つまり
\left\{ \begin{array}{c} C \equiv P + 3 \\ P \equiv C - 3 \end{array}\right.

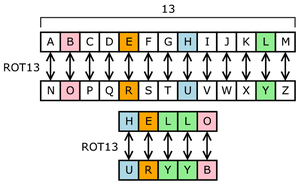
ROT13はこれと全く同じもので、鍵が13になったものである。

これを発展させた鍵つきシーザー暗号は、
d=eであり、
\left\{ \begin{array}{c} C \equiv P + e \\ P \equiv C - d \end{array}\right.
上記の物や平文を含め、26通りある。

アフィン暗号(Affine cipher)

シーザー暗号をより一般化したもので、
A=0,B=1,...,Z=25
とおいたとき、これらの文字を一次変換して26を法とする世界で変換する。
ここで、aを26より小さい、26と互いに素の数だとすると、必ず、
aA \equiv 1\bmod 26
を満たす整数Aが存在するから、これを用いると、
暗号鍵e_1,e_2(e_1は25以下の数で、26と互いに素)に対して、復合鍵d_1,d_2は、
\left\{ \begin{array}{c} e_1d_1 \equiv 1\bmod 26 \\ d_2 = e_2 \end{array}\right.
を満たす。これらを用いて、
\left\{ \begin{array}{c}C \equiv e_1P+e_2\bmod 26 \\ P \equiv d_1C - d_2\bmod 26 \end{aray}\right.
なぜならば、P \equiv AC \equiv aAP \equiv P となるからである。
e_1=1,3,5,7,9,11,15,17,19,21,23,25の12通りより、
平文を含め、暗号化のパターンは12\times 26=312通り

ヴィジュネル暗号

鍵を行列(matrix)にしたものである。
n×1行列Eを用いることで、n文字の暗号を一度に変換できる。
つまり、
E= \left( \begin{array}{c} w_1 \\ w_2 \\ \vdots \\ w_n \\ \end{array}\right)
が暗号カギであり、複合鍵はD=Eである。今、
P= \left( \begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \\ \end{array}\right)
とおくと
\left\{ \begin{array}{c}C \equiv P + E \bmod 26 \\ P \equiv C - D \bmod 26 \\ \end{array}\right.

ヒル暗号(Hill cipher)

鍵を行列(matrix)にしたものである。
n×n行列Eを用いることで、n文字の暗号を一度に変換できる。
つまり、
E= \left( \begin{array}{cccc} w_{1,1} & w_{1,2} & \cdots & w_{1,n} \\ w_{2,1} & w_{2,2} & \cdots & w_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n,1} & w_{n,2} & \cdots & w_{n,n} \\ \end{array}\right) \bmod 26
が暗号鍵で、複合鍵は
D=E^{-1}
である。∴鍵となりうる条件は
dim|E| \neq 0
且つdim|E|が26と互いに素である必要がある。
これらより、今、
P= \left( \begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \\ \end{array}\right)
とおくと、
\left\{ \begin{array}{c} C \equiv EP \bmod 26 \\ P \equiv DC \bmod 26 \end{aray}\right.

トリップ

総当たり
perlにおける変換関数crypt(PASSWORD,SALT)を用いたものである。
2chにおいては、#abcdefghと入力した場合、
パスワードとして"abcdefgh"を、
ソルトとして"bc"を採用する。
ソルトはサイト側が自由に変えられるランダムな変数に変換されるため、
これが分からない限りはほぼ確実に解読はできないが、
2chにおいてはこれもパスワードの一環と言うことになる。
この2つの値を用いて変換した結果がトリップとなる。
以下はトリップ生成のプログラムである。 
$tripkey = "#istrip";  # トリップキー文字列（# 付き）
$tripkey = substr($tripkey,1);
$salt = substr($tripkey.'H.',1,2);
$salt =~ s/[^\.-z]/\./go;
$salt =~ tr/:;<=>?@[\\]^_`/ABCDEFGabcdef/;
$trip = crypt($tripkey,$salt);
$trip = substr($trip,-10);
$trip = '◆'.$trip;
print "$trip";

解読

単一換字式暗号

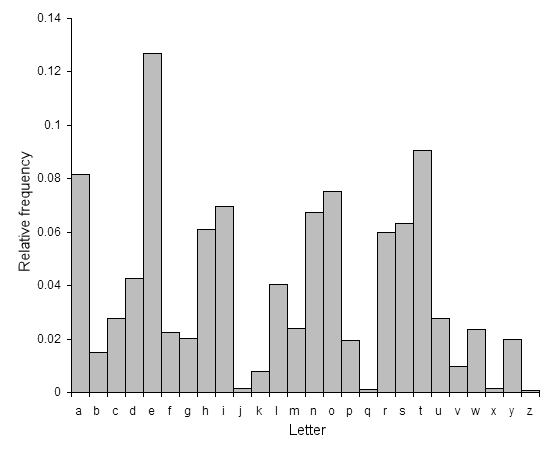
一般的に頻度分析を用いる。以下が英文における頻度分析の結果である。
なお、ヴィジュネル暗号などでも、THEなどの特定の単語に着目して
公倍数から鍵周期を特定すれば、間隔毎に頻度分析を用いることで解読できる。
エニグマ等のように十分に鍵周期の長い暗号文を除いては、全て解読可能と言うことになる。
アラビア語ではこのようになる。
スペイン語ではこのようになる。

タグ：

+ タグ編集
  • タグ：
タグの更新に失敗しました
エラーが発生しました。ページを更新してください。
ページを更新
「暗号」をウィキ内検索
最終更新：2012年01月07日 20:38
ツールボックス

下から選んでください:

新しいページを作成する
ヘルプ / FAQ もご覧ください。