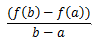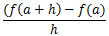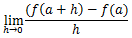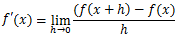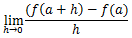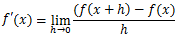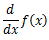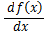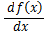微分係数、導関数 - 経済学メモ

経済学、特にミクロ経済学では微分を多用する。
ここでは、その微分について基礎からおさらいする。

• 微分係数
• 導関数

---

微分係数

あるグラフy=f(x)を考える。
そのグラフ上の2点A(a,f(a))、B(b,f(b))(a<b)を結ぶ直線を引く。
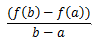
この直線の傾きはであり、これを平均変化率と呼ぶ。
この2点A、Bを限りなく近づけていくとどうなっていくだろうか。
ここではわかりやすくするためAを固定してBをAに近づけるとする。
b>aであるのである実数hを使ってb=a+hと表せる。
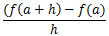
これを先ほどの平均変化率の式に代入すると、となる。
AとBを限りなく近づけていくためには、hを限りなく0に近づけていけばよい。
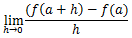
このことを記号でと書き表す。
これが微分係数である。
より簡略化した記号としてf'(a)を用いる。

また、f'(a)の値が存在する時、y=f(x)はx=aで微分可能という。
f'(a)はy=f(x)のx=aにおける接線の傾きに対応する。

導関数

微分係数はある定数aのみでの話である。
そこで、グラフ上の微分可能なすべてのxで成り立つようなものが欲しくなる。
それが導関数f'(x)だ。その定義式を書いておく。

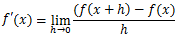
式の見た目自体は微分係数のaをxに変えただけにすぎない。
しかしその中身はかなり異なる。
aは定数であるが、xだと変数になる。
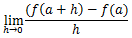
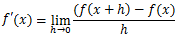
つまり、はただの値だが、は関数になる。
導関数の変数xにある値を代入したものが、その値での微分係数となる。

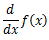
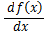
導関数のことは、f'(x)の他にや、と書くこともある。
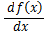
経済学では経験上f'(x)とがほとんどな気がする。論文などはわからないが。