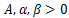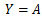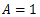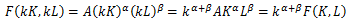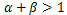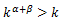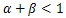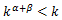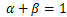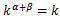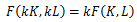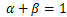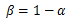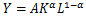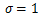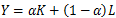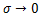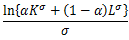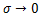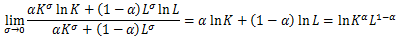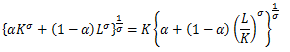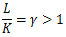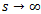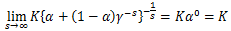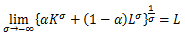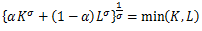コブダグラス関数、CES関数 - 経済学メモ

ここでは、生産関数や効用関数などとして使われるコブダグラス関数と、
コブダグラス関数を一般化したCES関数の基本性質について紹介する。

• コブダグラス関数
• CES関数

---

コブダグラス関数

を正の定数としたとき、の形で表される関数をコブダグラス関数という。
両辺の対数をとると、と対数の線形関数になる。

コブダグラス関数の形の生産関数はY:生産量、K:資本、L:労働として、
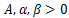
という形で表される。コブダグラス関数型なのでである。
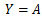
資本と労働を1単位ずつ投入したときには、だけ生産される。
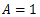
ここでYの単位をAにすれば、とすることができる。
このようなプロセスを正規化や標準化と言ったりする。

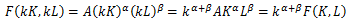
ここでKとLがk倍されたとすると、となる。
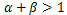
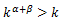
のとき、であるので…①となる。
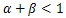
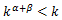
同様にのとき、であるので…②となり、
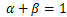
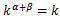
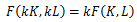
のときは、より…③となる。
①のときを規模に関して収穫逓増と呼び、②の場合を規模に関して収穫逓減と呼ぶ。
③の場合は規模に関して収穫一定と呼び、このときこの生産関数は1次同次である。
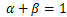
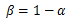
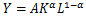
よりであるので、と表記できる。

CES関数

生産量Y、資本K、労働LとするとCES生産関数は、と表される。
このCES関数はコブダグラス関数を含んだより一般的な関数となっている。
CESとはconstant elasticity of substitutionの略で、「代替の弾力性が一定」という意味である。

CES関数は様々な関数を含んだ一般的な関数であるので、σの値によって様々な関数型になりうる。
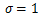
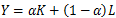
のとき、となって線形関数となる。

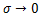
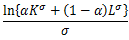
のとき、右辺の対数をとるととなる。
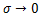
の極限をとるととなりロピタルの定理を用いて、
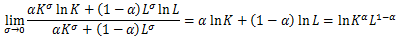
と変形される。
最初に対数をとっていたのでそれを元に戻すと、とコブダグラス型関数になる。

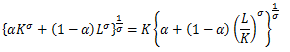
のとき、と変形できる。
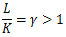
ここでと仮定し、、とおく。
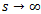
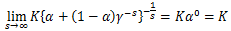
よりなので、となる。
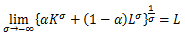
のときも同様にするととなり、
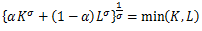
のときはである。