3次元凸包

という点が3次元空間に点在しているとします。
また

の座標は

という風に指定します。
ここで、「

の凸包

を求めよう」というのが今回の主題です。
点の数が多い-つまり

の数が多い-ことを想定して、分割統治法による解法を試みます。
1)

をx座標の大きい

とx座標の小さい

に分割します。
2)それぞれ

と

について、再帰的に凸法を作ります。
3)それらを統合します。
さて、1)2)のプロセスはいいでしょう。問題は3)のプロセス-つまり、分割した凸包をどうくっつけて凸包にするか-です。
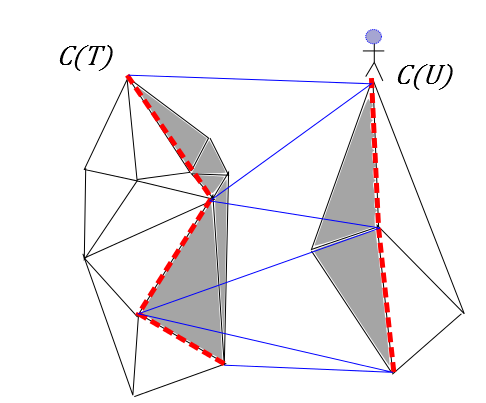
3次元凸包の統合
用語の定義をしましょう。図を見てもらうと棒人間が立っています。この人が色々な頂点から向こう側の3次元凸包を観察してみることができる三角形を灰色に塗りました。
言い換えれば、反対側の凸包からみて「オモテ側」の三角形ですね。
このオモテとウラの境目(図で赤い点線にしたところです。)をシルエットサイクルと呼ぶことにします。
これら2つの三次元凸包を統合したくば、「片方の凸包のシルエットサイクルに属す頂点」と「もう片方の凸包のシルエットサイクルに属す辺」で三角形をつくります。
こいつを接着剤代わりにして2つの凸包を繋ぐのです。この三角形を橋渡し三角形と言います。
ということで3次元凸包は結局橋渡し三角形を見つける問題に帰着されるわけです。
javascript plugin Error : このプラグインで利用できない命令または文字列が入っています。
最終更新:2012年10月24日 09:39