型 (Type) - TLA+メモ@ウィキ

型 (Type)

型の指定について

TLA+では、変数に対して明示的な型を指定することはない(型自体がないわけではない)。
一般的に変数に対する制約を述語や不変条件で表現する。

\inによる指定

例えば、以下ではxが1から3、yが1から5の整数であることを示している。このRangeInvariantは条件が満たされていればtrueを返す。

VARIABLES x, y
 
RangeInvariant ==
    /\ x \in {1,2,3}
    /\ y \in 1..5
 

上記を不変条件として検証を行うことは、変数xを1から3の値をとる整数型、変数yを1から5の値をとる整数型であることを定義することに等しい。

補足：
TLA+では範囲演算子を使用することができ、集合{1,2,…,n}を1..nのように定義できる。以下は同じ集合となる。

1..3 = {1,2,3} 

プリミティブ型 (基本的なデータ タイプ)

TLA+で利用可能な基本的なデータ型それぞれの特徴や使用方法を説明する。
TLA＋には、整数、ブール値、文字列、モデル値の4種類のプリミティブな型がある。

整数

EXTENDS IntegersでモジュールIntegersをロードすることで算術演算子 (+, -, %, *) を使用できる。除算は”\div”とあらわす。整数除算となる。

文字列

文字列は、文字のシーケンスを表現するために使用されるデータ型で文字列はダブルクォーテーションで囲まれた文字から構成される。
TLA+では、文字列の結合や部分文字列の取得などの基本的な文字列操作がサポートされる。

• 文字列は\o (または\circ)で連結することができる。
• 値vの文字列への変換はToString(v)を使用する。
• 文字列の長さはLen(s)で取得できる
• 部分文字列はSubSeq関数を使用して、文字列の部分文字列を取得することができる。SubSeq(s, m, n)は、文字列sのm番目からn番目の文字までの部分文字列を返す。

複合型

集合

集合は順序を持たない要素の集まりで、同じ要素を2つ持つことはない。集合内の要素の型はすべて同じでなければならない。
例えば以下のように定義できる。

set = {"a","b","c"} 

集合に対する演算子は以下がある。

演算子	意味	例
x \in set	集合setの要素x x ⊂ set	1 \in {1,2,3}
x \notin set	集合setの要素でないx x ⊄ set	4 \notin {1,2,3}
set1 \subseteq set2	set2の部分集合set1 set1 ⊂ set2	{1,2} \subseteq {1,2,3}
set1 \union set2	和集合 ※\cupも可	{1,2} \union {2,3} = {1,2,3}
set1 \intersect set2	積集合 ※\capも可	{1,2} \intersect {2,3} = {2}
set1 \ set2	差集合 set1 – set2	{1,2,3} \ {2} = {1,3}
SUBSET {"a", "b"}	冪集合	SUBSET {1,2} = {{}, {1}, {2}, {1,2}}
Cardinarity(set1)	要素数 (EXTENDS FiniteSetsが必要)	Cardinarity({1,2,3}) = 3

以下のように集合の変換を行うこともできる。

演算子	意味	例
{x \in set: 条件式}	フィルタリング 条件式を満たすsetの要素xを返す	{x \in 1..4: x < 3} >> {1, 2}
{式: x \in set}	マッピング setの要素xに対して式を適応する	{x * 3: x \in 1..3} >> {3, 6, 9}

タプル (シーケンス)

タプルは順序を持つ要素のコレクションで配列のようであるが要素の型は同じでなくてもよい。タプルのインデックスは1始まりとなる。
例えば tup = <<”a”, {1, 2}>> と記述した場合は、tup[1] = “a”, tup[2] = {1, 2}となる。

EXTENDS Sequences を指定することで次のシーケンス演算子を使うことができる。

演算子	意味	例
Head(seq)	先頭	Head(<<1, 2, 3>>) >>1
Tail(seq)	先頭以外	Tail(<<1, 2, 3>>) >> <<2, 3>>
Append(seq, x)	末尾に追加	Append(<<1, 2>>, 3) >> <<1, 2, 3>>
seq1 \o seq2	結合	<<1, 2>> \o <<3, 4>> >> <<1, 2, 3, 4>>
Len(seq)	長さ	Len(<<1, 2, 3>>) >> 3
SubSeq(seq, index1, index2)	スライス	SubSeq(seq, 1, Len(seq) - 1) >> 末尾の要素以外

タプルはシーケンスとも呼ばれるがシーケンス演算子を使う予定がない場合はタプル、シーケンス演算子を使う場合はシーケンスと呼ぶのが慣例となっている。

構造体 (あるいはレコード)

構造体は文字列に対して、値をマッピングすることができる。値へのアクセスは、struct.key でアクセスできる。

person = [name |-> "taro", age |-> 22, gender |-> "male"]
person.name
>> "taro"
 

struct.keyはstruct["key"]の糖衣構文なので以下でも同様となる。

person = [name |-> "taro", age |-> 22, gender |-> "male"]
person["name"]
>> "taro"
 

入れ子になった構造体には以下のようにしてアクセスできる。

struct = [ a |-> 1, b |-> [ x |-> 2, y |-> 3 ] ] 
struct.b.x
>> 2
 

関数

関数は一連の入力(定義域)を一連の出力にマッピングする。関数はすべて[x \in set |-> P(x)]の形式をとる。

入力
[x \in 1..2 |-> x*2]
 
出力
 <<2,4>>
 

TLA+における関数とは写像のことを意味している。一般的なプログラム言語で関数やプロシジャと呼ばれるものは演算子 (Operator)にあたる点に注意が必要。

演算子と異なり、定義域を指定する必要がある。

タプルと構造体

タプルと構造体は特別な関数である。タプルは定義域が1…nの関数であり、構造体は定義域が文字列の関数である。
そのため、タプル、構造体は関数と同様に操作することができる。

DOMAIN

DOMAINを使うことで関数の定義域(関数の入力としてとることのできる値の集合)を求めることができる。

DOMAIN [x \in 1..2 |-> x*2]
>>{1,2}
 

構造体に対しても同様にキーを取得することができる。

person = [name |-> "taro", age |-> 22, gender |-> "male"]
DOMAIN person
>>{"name", "age", "gender"}
 

関数と演算子の違い

• 演算子はある値を別の値に変換する。関数は、その定義域（ドメイン）内の各要素に対する値を返す。
• 関数がそのドメイン内の値に対してのみ定義されるのに対し、演算子は任意の値を入力に持つ。

関数の集合

[set1 -> set2] とすることでset1の要素をset2の要素にマッピングするすべての関数からなる集合を定義することができる。”|->”ではなく”->”である点に注意。関数の集合は複雑な仕様を書く際に役に立つ。

[{"a","b","c"}->{1,2}]
 
Value:
{ [a |-> 1, b |-> 1, c |-> 1],
     [a |-> 1, b |-> 1, c |-> 2],
     [a |-> 1, b |-> 2, c |-> 1],
     [a |-> 1, b |-> 2, c |-> 2],
     [a |-> 2, b |-> 1, c |-> 1],
     [a |-> 2, b |-> 1, c |-> 2],
     [a |-> 2, b |-> 2, c |-> 1],
     [a |-> 2, b |-> 2, c |-> 2] }
 

以下の値がタプルの集合となっているのは、タプルは定義域が1…nの関数であることから。

[{1,2}->{"a","b","c"}]
 
Value:
{ <<"a", "a">>,
     <<"a", "b">>,
     <<"a", "c">>,
     <<"b", "a">>,
     <<"b", "b">>,
     <<"b", "c">>,
     <<"c", "a">>,
     <<"c", "b">>,
     <<"c", "c">> }
 

関数の集合をうまく利用すると値同士の組み合わせのパターンを生成することができる。

定数 (Const)

定数を定義することもできる。

CONSTANT VALUE1, VALUE2 

上記の定義を追加すると後述のTLA+ToolBoxのModel Overviewに以下のように値が表示され、値を定義することができる。

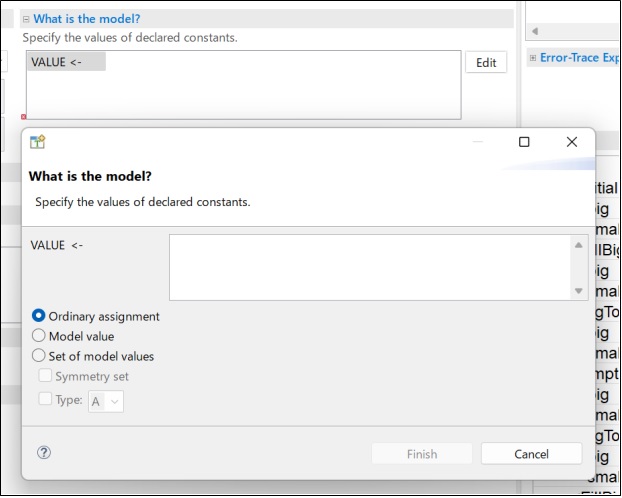
通常の割り当て (Ordinary assignment)

定数には、数値、集合、シーケンス、関数などTLA+のどの値でも設定できる。

Days <-1..31
CupSizes <- {“Short”, “Tall”, “Grande”, “Venti”}
 

モデル値 (Model Value)

定数にモデル値を代入することでその定数はそれ自身にのみ等しい値となる。つまり、C言語の列挙型のような抽象的なユーザー独自の定数を定義することができる。

facebook <- [ model value ]
User <- [ model value ]
 

Set of model values

Set of Model Valuesは、複数のModel Valueを含む集合を定数に割り当てることができる。

Apps <- [ model value ] {facebook, twitter, instagram}
Users <- [ model value ] {user1, user2}
 

定数の定義方法(2)

TLA+ToolBoxを使わず、値を設定することができる。例えば以下は名前が" Items "の定数を宣言し、定数に具体的な値を割り当てる。

CONSTANTS Items
Items == {“a”,”b”,”c”}
 

また、引数をとらず定数を返す演算子を定義することで実質的に定数として使うことができる。(CONSTANTSによる宣言をせず、直接下記を記述する。)

Items == {“a”,”b”,”c”}