Scene3　時間のおくれ

問題

　光速不変の原理を認めれば，最高の信頼性をもって時間をはかる方法として「光時計」を考えることができる。実用的ではないものの，時間というものに対する見方に革命的な変革をもたらした相対論のエッセンスを理解するのによいアイテムである。
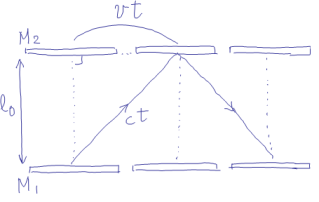
　しくみはいたって簡単。一定の距離 $l_0$ だけ離した鏡M $_1$ ，M $_2$ の間で光を往復させる。M $_1$ ，M $_2$ での反射が時を刻むというわけだ。この時計がたとえば右方向に速さ $v$ で運動しているときにどう見えるかを考えよう。

　この思考実験を考察する中で重大なパラドックスにつきあたるが，相対論によってそれが解決されるときに常識を超えた帰結がこぼれおちる。
　光時計が静止していれば，もちろん往復時間（周期）は，

$2t_0 = \frac{2l_0}{c}$

だが，これが右に速さ $v$ で動いていると，周期 $2t$ とおいて，

$\qquad (ct)^2 = l_0^2 + (vt)^2$
$\therefore \quad 2t = \frac{2l_0}{c} \times \frac{1}{\sqrt{1-\beta^2}}　，　\beta = \frac{v}{c}$

となって一見矛盾が生じる。でも私たちは，相対性原理と光速不変の原理のみを出発点として考えをすすめ，その結果の奇妙さはひとまず受容れてしまうべきなのだ。

$t = t_0 \times \frac{1}{\sqrt{1-\beta^2}} \qquad t_0 = t \times \sqrt{1-\beta^2} < t$

という結果は，運動する時計の周期は長くなり，静止した時計に比べてどんどんおくれていくことを示している。
　超高速リニアモーターカーがどんなスピードで走っていようと（ただし一定），乗っている君は慣性系にいるのだから，光時計は静止しているときと変わらぬ時を刻んでいるはずなのだった。ところが，駅のホームから通過する列車内の時計を見るとおくれているということだから，列車内に起こる現象のすべてがゆっくりと進むように見えると考えざるを得ない。そして，この奇妙な帰結こそが相対論の教える真実なのだ！　これを等速度系の「時間のおくれ」という。

練習問題 3

　速度 $v$ で動く光時計のおくれは直接には光速不変の原理の帰結である。「常識」的な（非相対論的な）考え方で光速が変化すると考えて，この光時計のすすみを考察してみよ（もちろん，その結論は相対性原理を破ることになる）。

タグ：

+ タグ編集

「Scene3　時間のおくれ」をウィキ内検索

最終更新：2009年04月20日 18:25

添付ファイル

科学のおもちゃ箱 @wiki