Scene4　ローレンツ短縮

問題

　こんどは，光時計の方向を90°回転させて，光の往復方向を速度$\vec{v}$の方向に一致させた場合に，光時計が刻む時間と光が進む距離の関係を考察してみよう。

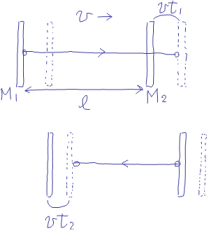
　あとの必要のため，M $_1$ ，M $_2$ 間の距離を（ $l_0$ ではなく） $l$ としておく。
　往路の所要時間 $t_1$ に対して，

$ct_1 = l + vt_1　\qquad \therefore \quad　t_1 = \frac{l}{c-v}$
　復路の所要時間 $t_2$ に対して，
$ct_2 = l - vt_2　\qquad \therefore \quad　t_2 = \frac{l}{c+v}$

だから往復の合計時間は，

$t = t_1 + t_2 = \frac{2cl}{c^2-v^2} = \frac{2l}{c} \times \frac{1}{1-\beta^2}　\quad ，\quad　\beta = \frac{v}{c}$

となる。しかし，ともに動く系で見た時計の刻み $t_0 = 2l_0/c$ に比べて，静止系から見たそれは

$t = \frac{t_0}{\sqrt{1-\beta^2}}$

というおくれを生じるのだった。以上のつじつまを合わせるためには，

$\frac{2l_0}{c} \times \frac{1}{\sqrt{1-\beta^2}} = \frac{2l}{c} \times \frac{1}{1-\beta^2}$

すなわち，

$l_0 = \frac{l}{\sqrt{1-\beta^2}}$
or
$l = l_0\sqrt{1-\beta^2} < l_0$

とする以外にない。つまり，光時計の長さがともに動く系で見た長さ $l_0$ （固有長）に対して $\sqrt{1-\beta^2}$ の比で短縮して見えるということを示す，これまた非常識な結果がこぼれ出た。これをアインシュタイン以前に理論的に導出したローレンツにちなんで，ローレンツ短縮と呼ぶ。
　上の考察でわかるように，ローレンツ短縮という帰結は時間のおくれと切り離せない関係にある。それらの間の深い関係は，次のSceneでより明らかにされるだろう。ちなみに，短縮は $\vec{v}$ の方向に起こるということを銘記しておこう。
　時間のおくれとローレンツ短縮で，ひとまずつじつまが合ったように思えるが，実は，以上の考察にはさらに深刻なジレンマが残されている。それは，往路時間 $t_1$ と復路時間 $t_2$ が等しくないということである。光時計とともに動く系では，この時間は等しく $l_0/c$ のはずだから， $t_1 &gt; t_2$ という結論にはさらに何らかの説明がないと納得できないだろう。次のSceneの中心テーマがこれにあたる。