Scene5　同時の相対性

問題

　超高速リニアモーターカーが速度 $\vec{v}$ で走っている。中央から　 $t=0$ に前後に発した光が前端および後端に達する現象を考察しよう。

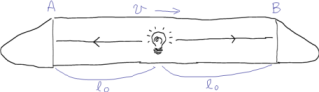
　ともに動く立場で見ればA，Bに達する時刻 $t_{0A}$ ， $t_{0B}$ は

$t_{0A} = t_{0B} = \frac{l_0}{c}$

で，もちろん列車に乗った君はその到達を同時であると見る。
　光時計の考察で計算ずみのように，これを地上の静止系から見ると

$t_A = \frac{l}{c+v} = \frac{l_0}{c} \times \frac{\sqrt{1-\beta^2}}{1+\beta} = \frac{l_0}{c} \times \sqrt{\frac{1-\beta}{1+\beta}}$
$t_B = \frac{l}{c-v} = \frac{l_0}{c} \times \frac{\sqrt{1-\beta^2}}{1-\beta} = \frac{l_0}{c} \times \sqrt{\frac{1+\beta}{1-\beta}}\quad ,\quad　\beta = \frac{v}{c}$

となる。ここで，ローレンツ短縮 $l=l_0\sqrt{1-\beta^2}$ を考慮した。
　明らかに $t_A&lt;t_B$ であるからA，Bへの光の到達は同時ではないことになる。2つのできごとが同時であるかどうかということが見る系によって変わるということになるのだ！中央からの光の発射が同時であることは疑うべくもない。光源を点灯したという事象はそれ自体ひとつのことだから。大切なのは，AとBのように離れた2点でおこる2つの事象が同時であるかどうかは自明でなく，見る系によって慎重に判断すべきだということなのだ。では，次の場合はどうだろう？

練習問題 5

　リニアモーターカーの中央に乗ったＴ氏は，「A，Bから『同時に』発した光が中央に『同時に』到達した」と主張する。地上の静止系からこれを見た君の主張はどうあるべきだろうか？

　さあ，時間のおくれ，ローレンツ短縮…ときてわかりかけた相対論だが，同時の相対性にいたってむしろ混迷を深めたのではないだろうか？　このジレンマを脱する道は，時間的な隔たりと空間的な隔たりを個別に考えるのでなく，統一的に考えるというところにある。

タグ：

+ タグ編集

「Scene5　同時の相対性」をウィキ内検索

最終更新：2009年04月21日 09:42

添付ファイル

科学のおもちゃ箱 @wiki