Scene6　時空のダイヤグラム

　列車のダイヤグラムというのがある。いわば運行予定表だが，時間とともに変化する複数の列車の位置がわかる。列車の走行を示す線が交差してダイヤの形◇がたくさんできるからそう呼ぶのかな？　これは，いわば $x-t$ グラフである。

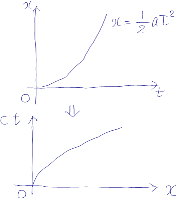
　たとえば，初速0で原点を出発した場合の等加速度運動の $x-t$ グラフは上のようになる。相対論では，一般に縦軸を時間軸にして上図下のように描く。これを時空のダイヤグラムと呼ぶことに異論はないだろう。横軸は $x$ 軸で代表させたが，本来 $x$ ， $y$ ， $z$ 軸がくる（平面上にはひとつしか描けない）。しばしば，縦横の軸のスケールを「長さ」に統一するために，時間軸は光速 $c$ をかけて表現することがある。
　リニアモーターカーの中央から発した光がA，Bで反射してもどるまでの光のダイヤグラムを描いてみよう。
　列車とともに動く系でのダイヤグラムは簡単だ。まさに，ダイヤの形そのままである。

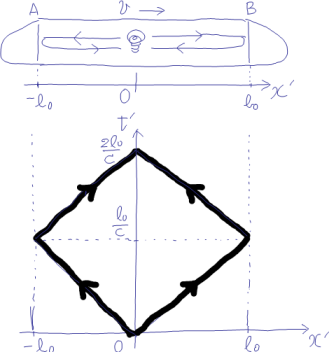
　地上から見た立場（静止系）ではどうなるだろう？
　まず私たちは，列車の運動をダイヤグラムに表現しなければならない。「A，中央，B」とした斜めの直線がそれである。AB間の $x$ 方向の間隔は， $2l=2l_0\sqrt{1-\beta^2}$ としてある。

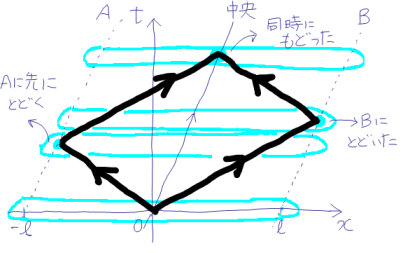
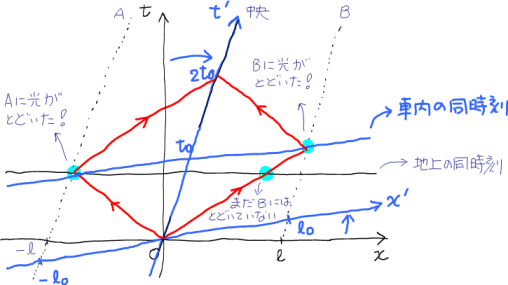
　光のダイヤグラムは，光速不変の原理によりどちらに向かうにも先ほどの「ともに動く系」のダイヤグラムと同じ傾き（ $\pm 1/c$ ）をもってのびていく。それは斜めにゆがんだダイヤ形になった！　もちろんA，Bへの光の到達は同時ではない！
　列車内ではこれが同時であることを考えると，外から私たちが見ている列車内は，その位置によって列車内の系（ともに動く系）における異なる時刻の状態を見ていることになるのだ !!

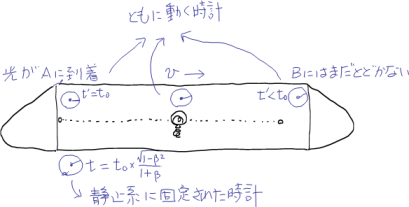
　列車内にずらりとならんだ時計があるとすれば，私たちが外から見ると少しずつ異なる時刻をさしていることになるわけだ。どうして列車が短く見えるのか，ローレンツ短縮の謎も解けたのではないだろうか？

練習問題 6

　上の図で，車内のAにある時計が時刻 $t_0$ をさしているならば，時間のおくれにより静止系の時刻 $t$ との関係は，

$t = t_0 \times \frac{1}{\sqrt{1-\beta^2}}$

となると思われるが，そうなってはいない。納得のいく説明を！

　以上の状況を時空のダイヤグラム上で見てみよう。地上の同時刻は下図の $x$ 軸に平行だが，車内の同時刻は図の $x^\prime$ 軸に平行になる。
　同一平面内で車内の時間‐空間座標軸を表現すると， $t^\prime$ - $x^\prime$ のような「斜交軸」となる。この軸上で， $t_0$ ， $l_0$ は図のようになる。ただし， $l=l_0\sqrt{1-\beta^2}$ などの長さの比は，この図の上でそのまま表現されてはいないので注意したい（これは $t$ 軸を $ct$ 軸にすれば解決するというようなものではない）。