Scene7　ローレンツ変換

　地上に静止した座標系をS， $x$ 方向に一定の速さ $v$ で走っているリニアモーターカーの車内に固定された座標系をS'としよう。

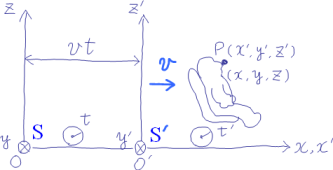
時刻 $t=t^\prime=0$ においてその原点OとO'が一致していたとして，

　Sの時空座標　 $(t,x,y,z)$
　S'の時空座標　 $(t^\prime,x^\prime,y^\prime,z^\prime)$

この両者を結ぶ変換は，相対性理論を考慮しなければ

$\left\{ \quad \begin{array}{l} t^\prime = t \\ x^\prime = x - vt\\ y^\prime = y \\ z^\prime = z \end{array} \right.$ 　　　　　

となり，これをガリレイ変換という。
　空間の等方性（特別の方向がなくいずれの方向も平等であること）から，相対性理論を考慮しても $y^\prime = y， z^\prime = z$ は変更を受けないが， $t^\prime$ と $x^\prime$ の式は修正される必要がある。
　まずもって変換は1次式になるだろう。なぜなら，逆に解いたとき（逆変換）に変わるのは相対速度の向きだけでほとんど同じ形になるはずだから。
　まず $x^\prime$ への変換は，ローレンツ短縮から

$x^\prime = \gamma(x-vt) \qquad ,　 \gamma = \frac{1}{\sqrt{1-\beta^2}} \quad , \quad \beta = \frac{v}{c}$

となりそうだ。S'の原点O'にあてはめれば， $x^\prime=0$ に対して $x=vt$ となるべきこともこれを支持している。

　逆変換は， $v$ が $-v$ におきかわるだけで，SとS'は対等平等だから，

$x = \gamma(x^\prime+vt^\prime)$

となるだろう。
　一方， $t^\prime$ への変換は時間のおくれから

$t^\prime = \gamma t + \alpha x$ 　　　（ $\alpha$ は $v$ のみの関数）

という形になると思われる。Sの原点にくっついた時計を考えると，つねに $x=0$ でこれをS'から見ると $\gamma$ の比でおくれているはずだから。また，これが $x$ を含むのが相対論の特徴で，車内の時計群が場所によって異なる時刻をさして見えるということに見合う形だ。
　さて， $\alpha$ を決めよう。 $t=t^\prime=0$ で一致した原点から $x$ 方向に発した光の到達点を考えると，S，S'から見て $x=ct$ ， $x^\prime=ct^\prime$ となる。これが変換式を満たすべきだから，

$\left.\begin{array}{lcr} x^\prime = \gamma(x-vt) \quad \longrightarrow \quad ct^\prime = \gamma(c-v)t \\ t^\prime = \gamma t + \alpha x \qquad \longrightarrow \quad t^\prime = (\gamma+\alpha c)t \end{array} \right\} \quad \therefore \quad　\alpha = -\gamma \, \frac{\beta}{c}$

結局，求める変換は

$\left\{ \quad \begin{array}{l} ct^\prime = \gamma (ct-\beta x) \\ x^\prime = \gamma (x - \beta ct) \qquad ,\quad　 \gamma = \frac{1}{\sqrt{1-\beta^2}} \quad , \quad \beta = \frac{v}{c} \\ y^\prime = y \\ z^\prime = z \end{array} \right.$