Scene8　速度の合成

問題

　どの慣性系で見ても光速は一定というのだから，速度の合成が相対論以前のように単にベクトルの和にならないことは明らかだ。 $x$ 方向に速度 $v$ をもつS'系から見た速度が $x^\prime$ 方向に $u$ である物体の，S系から見た速度 $w$ を求めよう。もちろん $w=u+v$ から修正を受けなければならないのだ。

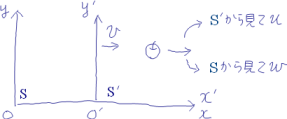
　S系とS'系の原点が一致した時刻 $t=t^\prime=0$ に，物体が $x=x^\prime=0$ を通過したものとすると，S'系で時刻 $t^\prime$ における位置は，

$x^\prime = ut^\prime$

となる。この物体の座標についてS系にもどせば，

$\left\{\begin{array}{l} x = \gamma(x^\prime+vt^\prime)=\gamma(u+v)t^\prime \\ t = \gamma(t^\prime+\displaystyle\frac{v}{c^2}x^\prime)=\gamma(1+\frac{uv}{c^2})t^\prime \end{array} \right.$

となるから，S系から見た物体の速度は

$w = \frac{x}{t} = \frac{u+v}{1+\displaystyle\frac{uv}{c^2}}$

これが目的の合成速度だ！
　光の場合は， $u=c$ を代入して

$w = \frac{c+v}{1+v/c}=c$

となる。光速がすべての慣性系で $c$ となり，また物体の速度が合成において決して $c$ をこえられないことがわかる。

練習問題 8-1

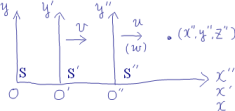
　S''系をS'系に対して $x^\prime$ 方向に速度 $u$ をもつ第3の慣性系とするとき，
　　S 　　　 $\longrightarrow$ 　　　S'　　　 $\longrightarrow$ 　　　 S''
　　　　　 $\beta=\frac{v}{c}}$ 　　　　　　 $\beta^\prime=\frac{u}{c}$
の2連続のローレンツ変換の結果が，
　　S 　　　 $\longrightarrow$ 　　　S''
　　　　　 $\beta^{\prime\prime}=\displaystyle\frac{w}{c}$
のローレンツ変換に一致することを確かめよ。

練習問題 8-2

　物体が $x$ 方向に垂直な速度成分をもつときは，合成速度はどうなるか？

タグ：

+ タグ編集

「Scene8　速度の合成」をウィキ内検索

最終更新：2009年04月22日 08:36

添付ファイル

科学のおもちゃ箱 @wiki