Scene10　エネルギーと質量

問題

　ふたたびScene9の問題にある完全非弾性衝突を考察しよう。

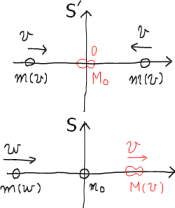
　S'系において合体・静止後の質量を $M_0$ とする。もちろん， $M_0=M(0)$ の意味だ。一方これをS系で見たとき，運動量保存により

$m(w)w = M(v)v$

となるべきだ。すると，

$M(v) = \frac{w}{v}m(w)$
　　　　 $= \frac{2v}{v\left( 1+\displaystyle\frac{v^2}{c^2}\right)}\cdot\frac{m_0}{\sqrt{1-\left(\displaystyle\frac{2v}{1+v^2/c^2}\right)^2/c^2}}$
　　　　 $= \frac{2m_0}{\sqrt{\left( 1+\displaystyle\frac{v^2}{c^2}\right)^2-\displaystyle\frac{(2v)^2}{c^2}}} = \frac{2m_0}{1-\displaystyle\frac{v^2}{c^2}}$

となる。しかし，

$M(v) = \frac{M_0}{\sqrt{1-v^2/c^2}}$

なのだから，

$M_0 = \frac{2m_0}{\sqrt{1-v^2/c^2}} = 2m(v)　！$

　 $M_0$ が $2m_0$ でなく，それより大きい $2m(v)$ になったというところに重大な帰結がある。 $M_0$ は静止質量だから，運動による質量の増大とは根本的にちがう。運動による質量変化は見る立場によって「そう見える」と解釈することもできるが，この場合は静止質量が $2m_0$ から $M_0$ に「正味」の増加をしたことになるのだ！
　S'系で見ると，衝突後運動エネルギーが0になるが，衝突前の運動の影響が， $M_0=2m(v)$ の形で引き継がれたことになる。明らかに運動エネルギーが質量に変わったように思われる！！
　 $v$ が小さいとして質量の変化を近似してみよう。

${\it \Delta} M = M_0 - 2m_0 &=& 2m(v) - 2m_0$
　　　　 $= 2m_0\left(\frac{1}{\sqrt{1-v^2/c^2}}-1\right)$
　　　　 $\fallingdotseq 2m_0\left(1+\frac{v^2}{2c^2}-1\right) = 2\times\frac{1}{2}m_0v^2/c^2$
　　　　 $= {\it \Delta}E/c^2$

　まさに運動エネルギーの減少分が質量に変わったということを意味する結果が得られた。これをふまえて，さらに質量とエネルギーは等価であるという飛躍を許せば，

$E = mc^2$ 　　（エネルギーと質量の等価性）

という有名な関係式にいたる。ここで $m$ は，

$m = \frac{m_0}{\sqrt{1-v^2/c^2}}$

であるから，

$E = mc^2 = \gamma m_0c^2 \quad ,\quad \gamma = \frac{1}{\sqrt{1-v^2/c^2}}$

そして $v\ll c$ のとき，

$E \fallingdotseq m_0c^2\left(1+\frac{v^2}{2c^2}\right) = m_0c^2 + \frac{1}{2}m_0v^2$
　　　　　　　　　　　　　　静止エネルギー　　運動エネルギー

となる。実際は，運動エネルギーの $\frac{1}{2}m_0v^2$ こそが近似であり，正しくは $(E-m_0c^2)$ である。
　最後にエネルギーと運動量の関係を導いて終わりにしよう。
　運動量は,　　　 $\boldsymbol{p} = \frac{m_0\boldsymbol{v}}{\sqrt{1-v^2/c^2}}$
　　　　　　　これによって運動方程式は，　　 $\frac{d\boldsymbol{p}}{dt} = \boldsymbol{F}$
　　　　　　　となる。質量も微分の中に入ることに注意!!