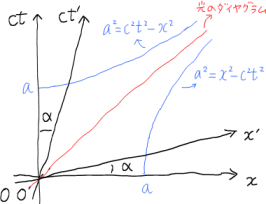
III．時空のダイヤグラム

　時空のダイヤグラムについて考察をしてみよう。

ローレンツ変換

$\left(\begin{array}{c}ct^\prime \\x^\prime\end{array}\right) = \left(\begin{array}{cc}\cosh\alpha \quad -\sinh\alpha \\-\sinh\alpha \quad \cosh\alpha\end{array}\right)\left(\begin{array}{c}ct\\x\end{array}\right)$

を3次元の回転と対応づけると，角 $\alpha$ は

$\tanh\alpha = \frac{\sinh\alpha}{\cosh\alpha} = \frac{\gamma\beta}{\gamma} = \beta$

これは図で $ct^\prime$ 軸が $ct$ 軸に対して， $\tan\alpha=\beta$ なる角 $\alpha$ だけ傾くことに対応する。
　一方， $x^\prime$ 軸も $x$ 軸に対して角 $\alpha$ だけ傾く。なぜならば， $x^\prime$ 軸上で

$ct^\prime = \gamma(ct-\beta x) = 0$ 　すなわち　 $\frac{ct}{x} = \beta$

となるから。空間の回転の場合とちがうのは， $ct$ 軸と $x$ 軸とで回転方向が逆な点だ。
　時空ダイヤグラムでもうひとつ注意しなければならないのは，その「スケール」だ。空間の距離にあたるインタバル $ds$ が，

$ds^2 = dct^2 - d\ve{r}^2$

となるから， $ct$ - $x$ 平面上において原点からの時間的インタバルが定数 $a$ である点の軌跡は，

$a^2 = ct^2 - x^2$

一方，原点からの空間的インタバルが一定である点の軌跡は，

$a^2 = x^2 - ct^2　（= -ds^2）$

すなわち，円ではなく双曲線となるのだ。
　原点から出る光のダイヤグラムは，原点が一致する時空座標系で常に $ct$ 軸と $x$ 軸のまん中を通り，その直線にそうどんなインタバルも0である。これは，光速で運動する時計は決して時を刻むことがないということだ！確かに固有時間は，

$d\tau = dt\sqrt{1-\frac{c^2}{c^2}} = 0$ 　（ $c^2d\tau^2 = ds^2$ に注目！）

タグ：

+ タグ編集

「III．時空のダイヤグラム」をウィキ内検索

最終更新：2009年04月24日 14:05

科学のおもちゃ箱 @wiki

III．時空のダイヤグラム

III．時空のダイヤグラム

メニュー

更新履歴