【解答】テニスの壁打ち - 科学のおもちゃ箱 @wiki - atwiki（アットウィキ）

科学のおもちゃ箱 @wiki

科学のおもちゃ箱 @wiki

【解答】テニスの壁打ち

打ち出しからもどるまでの運動の全過程は，地面から打ち出して地面にもどる過程の切り貼りになっていることがわかる（壁に衝突後は裏返し）。全過程の所要時間を $T$ とすると，これは最高点 $H$ からの自由落下時間の２倍に等しいから，

$H = \frac{1}{2}g\left(\frac{T}{2}\right)^2 \qquad \therefore T = 2\sqrt{\frac{2H}{g}}$

最高点 $H$ は，最高点までの所要時間 $t$ とするとき，

$v_0\sin\theta-gt=0,\qquad \therefore t = \frac{v_0\sin\theta}{g}$

より，

$H = h + v_0\sin\theta\cdot t - \frac{1}{2}gt^2 = h + \frac{v_0\;^2 \sin^2\theta}{2g}$

である。全過程の水平方向の移動距離は，

$v_0\cos\theta\cdot T = 2l$

であるから，上の結果を代入して整理すると，求める条件は

$v_0\cos\theta\sqrt{2gh+v_0\;^2\sin^2\theta} = gl$

となる。

(1) $l=\alpha h\quad (\alpha=5)$ として $\theta=30$ °を代入すると，

$v_0\;^4+8ghv_0\;^2-\frac{16}{3}\alpha^2g^2h^2 = 0$

これを $v_0$ について解くと，

$v_0 =2\sqrt{\left(-1+\sqrt{1+\frac{1}{3}\alpha^2}\right)gh}=2\sqrt{\left(-1+\frac{2\sqrt{21}}{3}\right)\cdot9.8}=9.0$ m/s

したがって，シミュレーションでは初速度を

$\boldsymbol{v}=(7.8,4.5)$

とすればよい。

(2) 上で求めた条件を $\sin\theta$ について整理すると，

$\sin^4\theta - \left(1-\frac{2gh}{v_0\;^2}\right)\sin^2\theta - \frac{2gh}{v_0\;^2} + \frac{\alpha^2g^2h^2}{v_0\;^4} = 0$

となる。数値代入すると，

$\sin^4\theta - \frac{4}{5}\sin^2\theta + \frac{1}{20} = 0$
$\therefore \sin\theta = \pm\sqrt{\frac{4 \pm \sqrt{11}}{10}} = \pm0.855,\pm0.261$
$\therefore \theta = \pm58.8$ °, $\pm15.2$ °

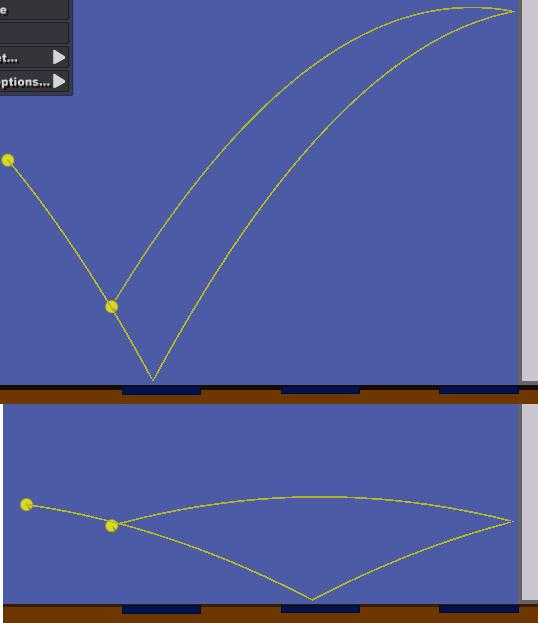
$\theta>0$ の場合のシミュレーション結果は下のようになった。 $\theta<0$ の場合も同様で，逆コースをたどるのみである。

タグ：

+ タグ編集

「【解答】テニスの壁打ち」をウィキ内検索

最終更新：2009年11月15日 16:20

添付ファイル

tennis2.JPG