安定を無視したつりあい問題

安定を無視し，単に力のつりあい条件のみで「静止」を語る悪問が後を絶たない。現実にありえない状態を問題にするのはいかがなものか？

OKWaveの質問から。

【問題】３つの点電荷 $q_1,q_2,q_3$ が一直線上に等間隔に並んで静止している。 $q_2 = +1{\rm [C]}$ として $q_1,q_3$ を求めよ。

【解答】
$q_2$ が受ける力のつりあいから，

$q_1q_2 - q_2q_3 = 0\qquad\therefore q1 = q3$

これは対称性からも明らかである。 $q_3$ が受ける力のつりあいから，

$q_2q_3 + \frac{1}{4}q_1q_3 = 0\qquad\therefore q_1 = q_3 = -4q_2 = -4{\rm [C]}$

アーンショーの定理から，静電気力のみによって点電荷が安定してつりあいを保つことはできない。明らかに上のような点電荷の配置は，不安定である。つまり，つり合い位置からのわずかな変位によって，系のつりあいは自ら崩壊するのである。上のつり合い配置において，系のポテンシャルエネルギーは極大となる。

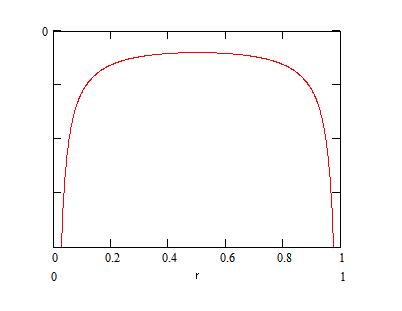
$q_1,q_3$ を間隔1に固定したとき， $q_2$ が $q_1,q_3$ を結ぶ線分上を動くときの位置エネルギーの変化

タグ：

+ タグ編集

最終更新：2010年10月01日 12:26

添付ファイル

科学のおもちゃ箱 @wiki