抵抗を受けるロケットの運動方程式 - 科学のおもちゃ箱 @wiki - atwiki（アットウィキ）

科学のおもちゃ箱 @wiki

科学のおもちゃ箱 @wiki

抵抗を受けるロケットの運動方程式

速度に比例する抵抗を受けるロケットの運動を調べる。Yahoo!知恵袋より。

なかなかおもしろい試み。質問者が提起した運動方程式は，

$(M_0-mt)\frac{dv}{dt} = F-\gamma v$

ただし， $M_0$ はロケットの初期質量， $m$ は単位時間当たりの噴出質量， $F$ は一定の推進力， $\gamma v$ は速さ $v$ に比例する抵抗力である。ロケットのような高速では，空気抵抗は速さの２乗（超）に比例するとされるが，まあ野暮なことはいうまい。初めこれを見たとき，質量を微分の中に入れなくていいのか？　と疑問に思った。しかしよく考えてみるとこれでよい。空気抵抗がなく，ロケットに対するガス噴出速度 $u$ が一定のときは，運動量保存により，

$Mv = (M+dM)(v+dv) - dM(v-u)$

すなわち，

$Mdv + udM = 0\qquad\therefore dv = -u\frac{dM}{M}$

初期条件 $v(0)=0$ の下に積分すると，

$v(t) = u \ln\frac{M_0}{M(t)}$

となる（ツィオルコフスキーのロケット方程式）。このプロセスで，

$M\frac{dv}{dt} = -u\frac{dM}{dt}$

を得るが，右辺が噴出ガスから受ける反作用すなわち推進力なのだ。 $M=M_0-mt$ すなわち $m=-dM/dt$ を用いれば，

$F = mu$

である。

さて，主題にもどって積分をしてみよう。

$(M_0-mt)\frac{dv}{dt} = F-\gamma v\quad{\rm i.e.}\quad\frac{dv}{F - \gamma v} = \frac{dt}{M_0-mt}$

対称的でわかりやすい（この気持ちいい対称性があったので，あえて２乗比例に持ち込まなかった）。初期条件 $v(0)=0$ として積分して，

$\frac{1}{\gamma}\ln\frac{F}{F-\gamma v} = \frac{1}{m}\ln\frac{M_0}{M_0-mt}$

$v$ について解くと，

$v = \frac{F}{\gamma}\left[1 - \left(\frac{M_0 - mt}{M_0}\right)^{\gamma/m} \right]$

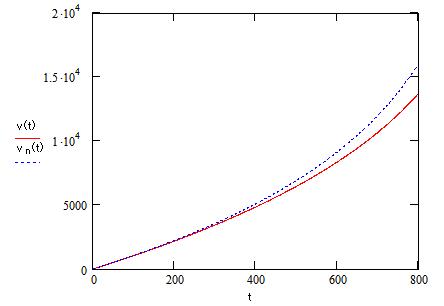
を得る。下図は，適当な数値を入れて抵抗の有無を比較したものである。

タグ：

+ タグ編集

「抵抗を受けるロケットの運動方程式」をウィキ内検索

最終更新：2010年11月11日 16:53

添付ファイル

Rocket.JPG