科学のおもちゃ箱 @wiki
科学のおもちゃ箱 @wiki
電気力線の方程式
絶対値の異なる正負の電荷対がつくる電気力線に関する問題。
問題を転載させていただいた。
真空中の電界について述べた次の文中の(a)(b)に適する式を答えよ。

クーロンの法則の比例定数をkとすれば、電気量Qの点電荷から距離rの点の電界の強さはk|Q|/r^2 , 無限遠を基準とした電位はkQ/rと表される。いま、電界の強さがEのところでは、電界の向きに垂直な断面1m^2当たりE本の電気力線を引くことにする。このようにきめると、点電荷Qを中心とする半径rの球面を通過する電気力線の総数は、ガウスの法則より4\pi k|Q|となる。
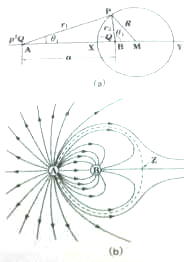
図(a)に示すように、距離がa離れた2点A,Bにそれぞれ電気量がp^2Q, -Qの点電荷が置かれている。ここでp > 1,Q > 0とする。
2点A,Bからそれぞれr_1,r_2の距離にある点Pの電位はkQ(p^2/r_1-1/r_2)となる。
したがって、r_1/r_2=p^2となる点の電位は0となる。
このように、2点A,Bからの距離の比が一定となる点の軌跡は、線分ABをこの比に内分および外分する2点X,Yを直径とする球面である。
この球の中心Mから点Bまでの距離は、pと球の半径Rを用いてR/p^2と表される。
電界の強さが0となる点をZとすると、BZ間の距離はa/(p-1)と表され、点Zの電位はkQ(p-1)^2/aとなる。
図のように角度\theta_1,\theta_2をとると、点Pを通る電気力線の方程式は一般に次のように表される。
Q(p^2\cos\theta_1-\cos\theta_2)=K (Kは定数)
この方程式で表される電気力線の概略は図(b)のようになり、一本一本の電気力線を表す方程式の定数Kは異なる値をとる。
点Aから出ている電気力線の一部は点Bに終わっているが、一部は無限遠まで行っている。図中の破線で示したように、電界の強さが0となる点Zを通る曲線が、点Bに行くか無限遠まで行くかの境界になる。
その境界を表す方程式は( a )のようになる。
この境界線が点Aを出るときに直線ABとなす角を\alphaとすれば\cos\alpha=( b )となる。

【解答】
( a ) 点Zでは\theta_1=\theta_2=0だから，与式より
　K=Q(p^2-1)
\therefore p^2\cos\theta_1-\cos\theta_2=p^2-1
( b ) 境界線が点Aを出る時、\theta_1=\alpha , \theta_2=\piだから，
　p^2\cos\alpha+1=p^2-1
\therefore \cos\alpha=1-\frac{2}{p^2}

タグ：

+ タグ編集
  • タグ：
タグの更新に失敗しました
エラーが発生しました。ページを更新してください。
ページを更新
「電気力線の方程式」をウィキ内検索
最終更新：2009年03月07日 21:35
添付ファイル